Federated optimization survey(1)：联邦学习背景介绍和问题定义

最近的”A field guide to federated optimization”这篇工作为联邦优化的研究提供了一个很好的总结和梳理，文章内容就如何定义联邦优化中的问题、哪些约束可能与给定问题相关以及如何对联邦优化进行验证分析提供了实用的建议。可以作为研究人员设计和评估新的联邦学习算法的指南，以及联邦优化从业者的简明手册。

我将基于这个工作，梳理出关于联邦优化的关键内容，能够更好的理解这个研究领域的痛点与研究进展。主要分为以下几篇内容：

Federated optimization survey(1) 联邦学习背景介绍和问题定义
Federated optimization survey(2) 实用的联邦学习算法设计
Federated optimization survey(3) 联邦优化算法的评估
Federated optimization survey(4) 联邦优化系统的限制与具体实践
Federated optimization survey(5) 联邦优化理论
Federated optimization survey(6) 联邦学习中的隐私、鲁棒性、公平性和个性化

这篇为第一部分，将对联邦学习的研究背景和问题定义进行介绍。

本文由本人整理完成，引用的话标注来源，欢迎随意转载阅读^ - ^

1. 联邦学习简介

联邦学习 (Federated Learning) 无疑是当前人工智能领域的一匹“黑马”，它是AI建模”数据可用不可见”的关键技术，在私有数据交易市场上也极具潜力。

之前的博客对于联邦学习进行过介绍，这里再次给出关于联邦学习的简介，联邦学习是一种去中心化机器学习范式，能在保护参与训练的边缘节点数据隐私的情况下完成联合机器学习建模。论文”Advances and open problems in federated learning.”[1]为联邦学习提出了一个更广泛的定义：

联邦学习是一种机器学习设置，其中多个实体（客户端）在中央服务器或服务提供商的协调下协作解决机器学习问题。每个客户的原始数据都存储在本地，不会交换或传输；而集中的更新用于直接聚合来实现学习目标

隐含在这个定义中隐含了提供强大的隐私保护的目标，也是 FL 的核心动机。将数据存储在本地而不是在云中复制它，可以减少系统的攻击面，集中和短暂的更新以及尽快聚合遵循数据最小化的原则。当 FL 与差分隐私和安全多方计算 (SMPC) 协议（如安全聚合）等其他技术相结合时，可以实现更强的隐私属性。遵守这些隐私原则并确保与其他隐私技术兼容的需求对联邦优化算法的设计空间提出了额外的限制。

2.联邦优化

联邦优化需要解决集中式方法中通常不需要解决的许多问题，包括：

通信效率问题：联邦学习是一种分散数据的分布式计算范式。为了系统效率和支持联邦学习的隐私，需要最小化服务器和客户端之间的通信。当客户端是带宽和连接可用性有限的移动设备时（比如cross-device场景），通信可能成为主要瓶颈。
（数据）异构问题：联邦场景下，数据存储在客户端，并且由于隐私原因永远不会直接与服务器或其他客户端通信。数据量通常是高度不平衡的（客户端具有不同数量的训练数据）和统计异质性（客户端的训练样本可能来自不同的分布）。当目标是为所有客户端训练单个全局模型时，尤其是在通信预算有限的情况下，联邦设置中的Non IID数据分布具有一定的挑战性
计算限制问题：由于固有的硬件差异，或由于相互竞争的后台任务，客户端可能具有不同的本地计算速度，这可能导致具有挑战性的计算异构性
隐私和安全问题：隐私是联邦学习设置中的一个明确目标，FL 本身的定义表明，出于这个原因，算法应该限制自己只能通过聚合访问数据中的信息。
系统复杂性：实际的 FL 系统通常很复杂，系统的稳健必须依赖于不同 FL 组件的密切协作，例如用于数据存储和本地计算的客户端、用于收集和传输信息的通信通道和聚合器，以及用于协调和全局计算的服务器。

3.联邦应用场景

联邦学习的应用场景中主要有两个算法设计设置：cross-device FL和cross-silo FL。cross-device FL的目标是跨大量移动设备的机器学习，而cross-silo联邦学习的目标是多个组织之间的协作学习。跨设备和跨孤岛联邦优化都具有数据和计算异构性以及通信和隐私约束，但它们也有一些方面的差异：

客户端的数量： cross-device FL中的客户端总数通常比cross-silo FL大得多。cross-silo FL中的客户端（组织）数量可能只有两个，更常见的是几十个或数百个，而cross-device FL中的客户端（设备）数量很容易超过数百万。
客户端的可用性： Cross-silo 客户端通常托管在数据中心，这意味着所有客户端都能参与每一轮训练。相比之下，典型的cross-device FL设置下具有大量且间歇性可用的客户端，意味着服务器只能通过一定的采样过程来访问客户端，且控制客户端的能力有限，同时客户端参与训练的可用性也可能与其本地训练数据分布相关
连接拓扑结构：直接对等连接在移动设备平台上通常得不到很好的支持，而在cross-silo FL设置中，这种直接的客户端到客户端连接可能更容易建立。在cross-silo FL 中，研究人员探索了多种通信模式，例如分散式 FL 、垂直 FL 、拆分学习和分层 FL。
计算和通信限制：跨设备设置中的计算和通信约束更加严格。边缘设备通常具有有限的计算和通信能力，而跨孤岛设置中的客户端通常可以是能够部署硬件加速器和高带宽通信链路的数据中心。
客户本地计算状态：在cross-device FL设置中，我们通常假设设备没有标识符，并且可能只参与整个训练过程一次，通常需要没有客户端状态的算法。相反，在cross-silo FL设置中，由于大多数客户端将参与大多数轮次的训练，因此可以采用带有状态的算法。

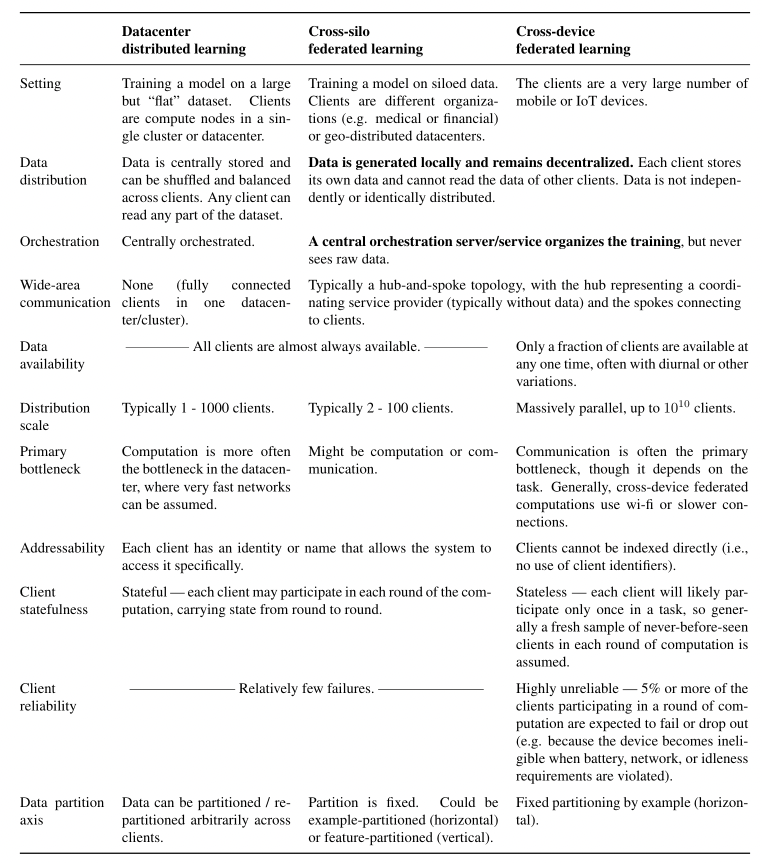
下面这个来自于[1]“Advances and Open Problems in Federated Learning”论文中的表格更为详细的对比分析了cross-device FL、cross-silo FL以及数据中心的分布式学习这三种学习场景：

4. 联邦学习问题定义

在联邦学习的基本概念中，我们希望最小化目标函数：

\[F(\boldsymbol{x})=\mathbb{E}_{i \sim \mathcal{P}}\left[F_{i}(\boldsymbol{x})\right], \quad \text { where } \quad F_{i}(\boldsymbol{x})=\mathbb{E}_{\xi \sim \mathcal{D}_{i}}\left[f_{i}(\boldsymbol{x}, \xi)\right] \qquad (1)\]

其中$\boldsymbol{x} \in \mathbb{R}^{d}$ 表示全局模型的参数，$F_{i}: \mathbb{R}^{d} \rightarrow \mathbb{R}$ 表示客户端$i$的局部目标函数，$\mathcal{P}$ 表示客户端集合 $\mathcal{I}$ 的总体分布。局部损失函数 $f_{i}(\boldsymbol{x}, \xi)$ 通常是所有客户端都相同，但本地数据分布$\mathcal{D}_{i}$ 经常会发生变化，体现了数据的异构性。

在cross-device 和cross-silo 设置中，(1) 中的目标函数可以采用具有有限客户端且每个客户端具有有限本地数据的经验风险最小化 (ERM) 目标函数的形式：

\[F^{\mathrm{ERM}}(\boldsymbol{x})=\sum_{i=1}^{M} p_{i} F_{i}^{\mathrm{ERM}}(\boldsymbol{x}), \quad \text { where } F_{i}^{\mathrm{ERM}}(\boldsymbol{x})=\frac{1}{\left|D_{i}\right|} \sum_{\xi \in D_{i}} f_{i}(\boldsymbol{x}, \xi) \text { and } \sum_{i=1}^{M} p_{i}=1 \qquad(2)\]

请注意，$M$ 表示客户端总数，$p_{i}$ 是客户端 $i$ 的相对权重。设 $p_{i}=D_{i} / \sum_{i=1}^{M}D_{i}$使目标函数$F^{\text {ERM }}(\boldsymbol{x})$等同于所有局部数据集联合的经验风险最小化目标函数。如果我们随机选择一定数量的客户并从他们的本地数据集的联合构建一个中央训练数据集，并且进行集中优化，(1) 中的目标（在预期中）等同于 ERM 目标。与集中训练相比， (1) 和 (2) 的几个关键特性如下：

异构和不平衡数据：本地数据集$D_{i}$ 可以具有不同的分布和大小。因此，局部目标$F_{i}(\boldsymbol{x})$ 可能不同。例如，它们可能具有任意不同的局部最小值。
数据隐私限制：$D_{i}$ 的本地数据集不能与服务器共享或跨客户端打乱。
有限的客户端可用性 (在cross-device FL更常见):在跨设备 FL 中，(2) 中的客户端 M 的数量可能非常大，甚至不一定是明确定义的。一定时间内，只有一小部分客户端（通常少于 1%）可用于连接服务器并参与训练。客户端分布$\mathcal{P}$，客户端总数$M$ 或数据样本总数在训练开始之前是先验未知的。

5. FedAvg: 联邦平均算法

求解 (1) 的常用算法是由 McMahan 等人提出 [2]的联邦平均 (FedAvg)。该算法将训练过程分成几轮，在第 t 轮开始时（t ≥ 0），服务器将当前全局模型 $\boldsymbol{x}^{(t)}$ 广播给一组参与者：客户端的随机子集 $\mathcal{S^{(t)}}$ （通常在模拟中均匀采样而不进行替换）然后，该轮队列中的每个采样客户端对其自己的本地数据集执行$\tau _i$ 个本地 SGD 更新，并将本地模型更新$\Delta_{i}^{(t)}=\boldsymbol{x}_{i}^{\left(t, \tau_{i}\right)}-\boldsymbol{x}^{(t)}$ 发送到服务器。最后，服务器使用聚合的 $\Delta_{i}^{(t)}$ 更新全局模型： $\boldsymbol{x}^{(t+1)}=\boldsymbol{x}^{(t)}+\frac{\sum_{i \in \mathcal{S}^{(t)}} p_{i} \Delta_{i}^{(t)}}{\sum_{i \in \mathcal{S}^{(t)}} p_{i}},$ 其中 $p_i$ 是客户 $i$ 的相对权重。上述过程将重复进行，直到算法收敛。在所有客户都参与每一轮训练的cross-silo设置中，有$\mathcal{S}^{(t)}=\{1,2, \ldots, M\}$ 。

FedAvg 可以很容易地推广到一个灵活的框架，允许算法设计者更改客户端更新规则、全局模型的更新规则，或应用于更新的聚合方法。特别是，Reddi et al. [3] 提出了 FedAvg 的通用版本，其伪代码在算法 1 中给出。该算法由两个基于梯度的优化器参数化：ClientOpt 和 ServerOpt，分别具有客户端学习率 $\eta$ 和服务器学习率 $\eta_S$ 。 ClientOpt 用于更新局部模型，而 ServerOpt 将聚合局部更新的负值 $-\Delta^{\left(t\right)}$ 视为伪梯度，并将其应用于全局模型。

FedAvg 算法可以看作是 Local SGD的推广，它被研究用于降低经典分布式设置中的通信成本。 FedAvg 的一些显著特性是，与经典的分布式设置不同，只有一部分客户端参与每一轮训练。在分析方面，本地 SGD 的收敛分析通常假设本地数据是同质的，并且每个客户端执行相同数量的本地更新，这在联邦设置中可能不成立。

Reference

[1] Peter Kairouz, H Brendan McMahan, Brendan Avent, Aur ́elien Bellet, Mehdi Bennis, Arjun Nitin Bhagoji, Keith Bonawitz, Zachary Charles, Graham Cormode, Rachel Cummings, et al. Advances and open problems in federated learning. arXiv preprint arXiv:1912.04977, 2019.

[2] H Brendan McMahan, Eider Moore, Daniel Ramage, Seth Hampson, and Blaise Aguera y Arcas. Communication-efficient learning of deep networks from decentralized data. In Proceedings of the 20th International Conference on Artificial Intelligence and Statistics, pages 1273–1282, 2017. Initial version posted on arXiv in February 2016.

[3] Sashank J. Reddi, Zachary Charles, Manzil Zaheer, Zachary Garrett, Keith Rush, Jakub Koneˇcn ́ y, Sanjiv Kumar, and Hugh Brendan McMahan. Adaptive federated optimization. In International Conference on Learning Representations, 2021. URL https://openreview.net/ forum?id=LkFG3lB13U5.