Deep Leakage in Federated Learning

Posted on | In |

数据交易流通是数据市场建立的关键技术，同时带来了一定安全问题，如数据滥用和信息泄露。为了在推动数据流动的同时保护数据安全、个人信息和隐私，隐私计算技术应运而生。联合学习（FL）作为一种保护隐私的分布式学习范式，已经获得很多研究者的关注，它通过共享和聚合本地模型而不是本地数据来提高全局模型的性能，以保护用户的隐私。尽管对原始数据的访问受到限制，但最近的工作表明，FL也面临着各种隐私攻击，已经有一系列关于在FL场景下基于共享梯度和权重重建训练数据的研究。这种重构攻击值得深入研究，因为它可以发生在训练的任何阶段，无论是在模型训练的开始还是结束时；不需要相关的数据集，也不需要训练额外的模型。本文主要回顾了三种基于联合学习的深度泄漏攻击算法，包括Deep Leakage from Gradients(DLG)、 improved Deep Leakage from Gradients(iDLG)和Inverting Gradients(IG)，进一步分析和总结FL深度泄露的更多改进工作，以及强调不要仅仅依靠联邦学习机制来提供隐私保证的重要性。

本文内容由本人整理分析，未经作者同意禁止转载。

概述

背景

数据是人工智能的燃料。优秀的深度学习模型需要依靠大量的高质量数据集进行训练。然而，随着模型精度的不断提高，个人隐私的泄露问题也越来越严重。社会对隐私的关注，带来了世界范围内数据保护立法的出现，如欧盟的GDPR，美国的HIPAA法案和英国的数据保护法（PDA）。由于在数据收集和共享过程中存在潜在的隐私泄露风险，集中式机器学习方法正变得不安全。

在许多应用场景中，机器学习中的训练数据是隐私敏感的。例如，一个病人的医疗状况不能在各医院之间共享。联邦学习是一个具有隐私保护的分布式机器学习框架，旨在让分散的各方协同进行模型训练，而不向其他参与者披露私人数据，受到了广泛的关注。一个典型的联邦学习训练过程会重复五个步骤：客户端选择、广播、客户端计算、聚合和模型更新。在联邦随机梯度下降法（FedSGD）和联邦平均法（FedAvg）的基本设置中，每个设备在本地数据上进行学习，并共享梯度或权重以更新全局模型。无需传输训练数据提供了几个关键优势，首先这可以保持用户数据的私密性，缓解用户隐私安全和数据所有问题相关的担忧，以及这消除了存储、传输和管理大型数据集的需要。

在联邦学习场景下尽管限制了对原始数据的访问，但最近的工作表明，FL也面临着各种隐私攻击，如成员推理攻击，属性推理攻击，它们可以推断出训练数据的一些信息。最近的攻击方法，如梯度深度泄露（DLG），改进的梯度深度泄露（iDLG），反转梯度（IG），已经证明了从模型更新中完全重建训练数据的可能性，这可能是非常危险和具有挑战性的攻击，所能造成的后果严重。

联邦学习

一般来说，联邦学习可以分为两类：有参数服务器（集中式）和没有参数服务器（分布式）。在这两种的学习范式中，每个节点首先进行训练计算更新其本地权重，然后将梯度传送给其他节点。对于中央模式，更新的梯度先被聚集，然后被传回每个节点；对于分布模式，梯度在相邻节点之间交换，这更容易导致隐私泄露，因为任何参与者都可以窃取其邻居的私有训练数据。因此对于联邦学习场景下的梯度泄露攻击。主要集中在更普遍和严格的中央模式上。

在FL中，中央服务器将当前模型广播给每个客户端，每个客户端将在其本地数据上训练模型。在每一轮通信中，中央服务器将把梯度或权重从一个客户子集更新到全局模型中，根据传输的是梯度还是权重分别对应于FedSGD和FedAvg

假设共享的模型架构为\(F\)，在第\(t\)轮的通信轮次中，全局模型的参数是\(W_t\)，本地模型的参数为\(W_i^t\)，在第\(i\)个节点上的训练数据为\((x_i,y_i)\)，本地模型计算本地的参数更新：

\[\nabla W_{i}^{t}=\frac{\partial \mathcal{L}\left(F\left(x_{i}^{t}, W^{t}\right), y_{i}^{t}\right)}{\partial W^{t}}\]

FedSGD \(\begin{aligned} \nabla W^{t} &=\frac{1}{N} \sum_{i}^{N} \nabla W_{i}^{t} \\ W^{t+1} &=W^{t}-\eta \nabla W^{t} \end{aligned}\)

FedAvg \(\begin{aligned} W^{t+1} &=W^{t}-\eta \nabla W^{t} \\ \nabla W^{t+1} &=\frac{1}{N} \sum_{i}^{N} \nabla W_{i}^{t+1} \end{aligned}\)

Threat Model

在这个问题场景中，Threat Model是诚实而好奇的服务器。它的目标和能力是进行数据重建攻击，这是一种白盒攻击。攻击者知道模型的架构、优化细节、损失函数和超参数，如学习率、批次大小等。

首先考虑一个攻击场景，从单一样本的梯度重建原始图像，即给定一个服务器模型及其权重，当服务器获得单一输入数据\((x,y)\)对应的梯度时，可以重构输入数据。这是简化的FedSGD场景，也是最简化的数据重建攻击场景，它对应的是能够通过这种攻击手段重建的数据质量的上限。

第二种攻击场景是从批数据的平均梯度重建原始图像。与上述攻击场景不同的是，其中一个样本需要基于多个数据的平均梯度进行重建。因为在DLG研究中表示如果基于N个样本的平均梯度来重建相应的N个样本的算法会运行起来太慢，无法收敛。但是这种情况比上述情况更常见，它对应的是通用的FedSGD算法。

第三种攻击场景是通过权重重建图像，这是一种基于FedAvg算法架构的攻击，即给定一个服务器模型及其权重，当服务器获得与输入数据\((x,y)\)相对应的更新权重时，它可以重建输入数据或泄露一些信息。

DLG: Deep Leakage from Gradients

首先介绍的是论文[1]提出的DLG方法。它是第一个基于梯度的样本重建攻击方法，能够仅仅通过在同重神经网络上的梯度共享来完全重建一个隐私数据集。这项技术由于用户数据隐私而带来了 “深度 “威胁，被称为 “梯度深度泄漏”（DLG）。

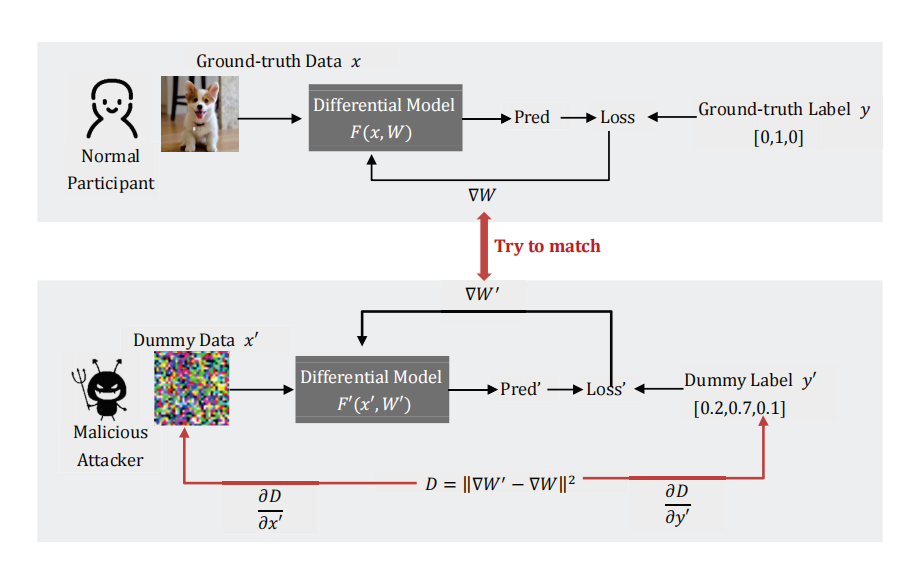
image-20220329113414508

DLG算法的概述：当正常参与者使用其私有训练数据计算\(W\)以更新参数时，恶意攻击者通过更新其假输入和标签来最小化真实梯度和虚拟梯度间的距离。当优化完成后，恶意用户就能从诚实的参与者那里获得训练集。

假设能够获得共享梯度参数的一方是一个恶意攻击者，他收到了其他参与者\(k\)在第\(t\)轮的梯度更新，并试图从共享信息中窃取参与者k的训练集。上图显示了整体攻击过程。

该算法首先初始化一个与真实样本具有相同分辨率的虚拟图像\(x′\)，并基于概率表示法初始化一个虚拟标签\(y′\)和softmax层。由于大多数联合学习应用场景默认共享模型架构\(F()\)和权重\(W_t\)，这里也假设\(F()\)和\(W_t\)是两方都已知的。当攻击者发起攻击时，他将根据其本地模型上的假数据\(x\)和假标签\(y'\)来计算假梯度。这里的重建攻击的关键是反复优化虚拟图像和标签，使攻击者的虚拟梯度接近真实梯度。当梯度距离损失达到最小时，虚拟数据也将以高置信度收敛到训练数据。损失函数表达式如下: \(\begin{array}{r} x^{* \prime}, y^{* \prime}=\arg \min _{x^{\prime}, y^{\prime}}\left\|\nabla W^{\prime}-\nabla W\right\|^{2} \\ =\operatorname{argmin}_{x^{\prime}, y^{\prime}}\left\|\frac{\partial l\left(\mathrm{~F}\left(x^{\prime}, W\right) y^{\prime}\right)}{\partial W}-\nabla W\right\|^{2} \end{array}\) 算法1中展示了DLG的伪代码。事实上有很多因素会影响DLG方法数据重建的效果，如第2行的数据初始化，第5行的两个梯度之间的距离计算，以及第6行的优化方法。在某些情况下，DLG会由于某些原因而无法达到预期的效果，如不好的数据初始化。

image-20220329113317639

iDLG: Improved Deep Leakage from Gradients

上面介绍的DLG攻击是基于梯度和训练数据之间存在一对一映射的假设。因此，如果DLG没有找到真实数据，攻击就无法收敛。对于有交叉熵损失的任务，论文[2]提出了一个分析方案，即从共享梯度中提取真实标签。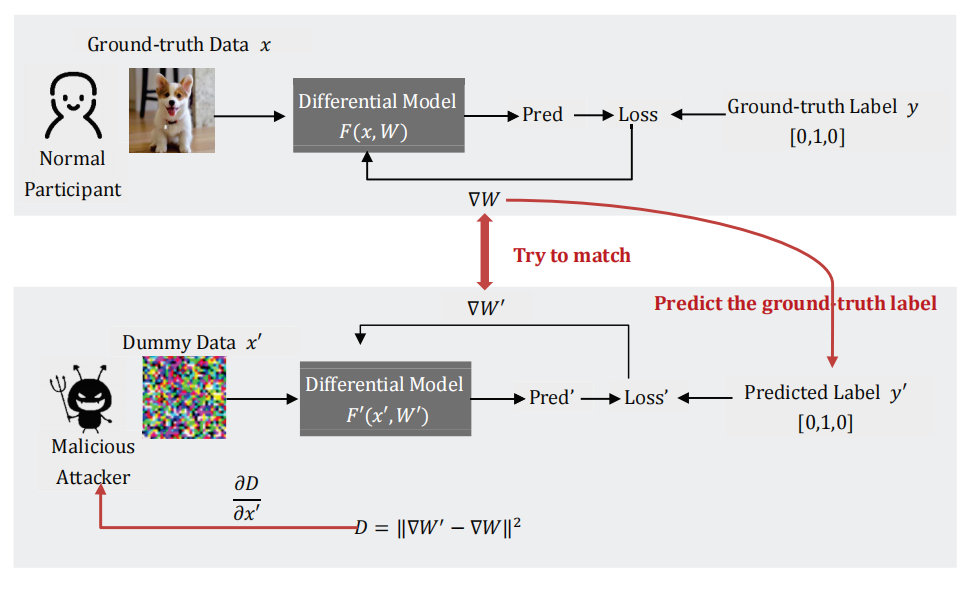当可微分模型在一个独热标签的监督下训练时，损失函数为： \(\begin{array}{r} x^{* \prime}=\arg \min _{x^{\prime}}\left\|\nabla W^{\prime}-\nabla W\right\|^{2} \\ =\operatorname{argmin}_{x^{\prime}}\left\|\frac{\partial l\left(\mathrm{~F}\left(x^{\prime}, W\right), y^{\prime}\right)}{\partial W}-\nabla W\right\|^{2} \end{array}\) image-20220329113459240

论文[2]中给出了相关证明了通过计算观察共享的梯度可以直接推导出真实的标签。基于提取的标签，泄漏过程将更加稳定和有效。它与DLG的主要区别在于，iDLG不生成基于概率的虚拟标签，而是从更新的梯度中推导出真实数据标签。对虚拟梯度和真实梯度之间距离的优化只基于虚拟数据\(X\)。结合上面的流程图，可以理解训练过程。算法2展示了iDLG算法的伪代码。

image-20220329113333693

IG: Inverting Gradients

前面介绍的两种方法DLG和iDLG是基于虚拟梯度和真实梯度之间的L2欧氏距离进行优化的。论文[3]提出的方法对它们做了两个主要修改：首先，作者认为重要的不是梯度的大小，而是梯度的方向。基于这一推理，使用了余弦距离的损失函数，鼓励攻击者找到导致相同梯度方向变化的样本进行重建。损失函数的表达式为： \(\underset{x^{\prime} \in[0,1]}{\operatorname{argmin}} 1-\frac{\left\langle\nabla_{\theta} L_{\theta}\left(x^{\prime}, y\right), \nabla_{\theta} L_{\theta}(x, y)\right\rangle}{\left\|\nabla_{\theta} L_{\theta}\left(x^{\prime}, y\right)\right\|\left\|\nabla_{\theta} L_{\theta}(x, y)\right\|}+\alpha T V\left(x^{\prime}\right)\) 此外，IG还提出了以下改进尝试（i）将搜索空间限制在[0, 1]，（ii）增加总变化作为图像先验，以及（iii）基于损失梯度的符号和ADAM优化器来最小化损失函数。这种修改的灵感来自于对DNN的对抗攻击，它使用类似的技术来产生对抗输入。

开源代码

Reference

Zhao, B.; Mopuri, K. R.; and Bilen, H. 2020. iDLG: Improved Deep Leakage from Gradients. CoRR, abs/2001.02610.

Zhu, L.; Liu, Z.; and Han, S. 2019. Deep Leakage from Gradients. In NeurIPS.

Geiping, J.; Bauermeister, H.; Dr¨oge, H.; and Moeller, M. 2020. Inverting Gradients - How easy is it to break privacy in federated learning? In Larochelle, H.; Ranzato, M.; Hadsell, R.; Balcan, M.; and Lin, H., eds., Advances in Neural Information Processing Systems 33: Annual Conference on Neural Information Processing Systems 2020, NeurIPS 2020, December 6-12, 2020, virtual.