PATE-GAN为一种确保生成对抗网络(GAN)框架生成器的(差分)隐私的方法,所得模型可用于生成合成数据,可在该合成数据上训练和验证算法,并在不影响原始数据集隐私的情况下进行算法性能对比。该方法修改了PATE框架,并将其应用于GAN。修改后的框架(称为PATE-GAN)能够紧密限制任何单个样本对模型的影响,形成严格的差分隐私保证,因此与具有相同保证的模型相比,性能得到了改善。
PATE-GAN模型
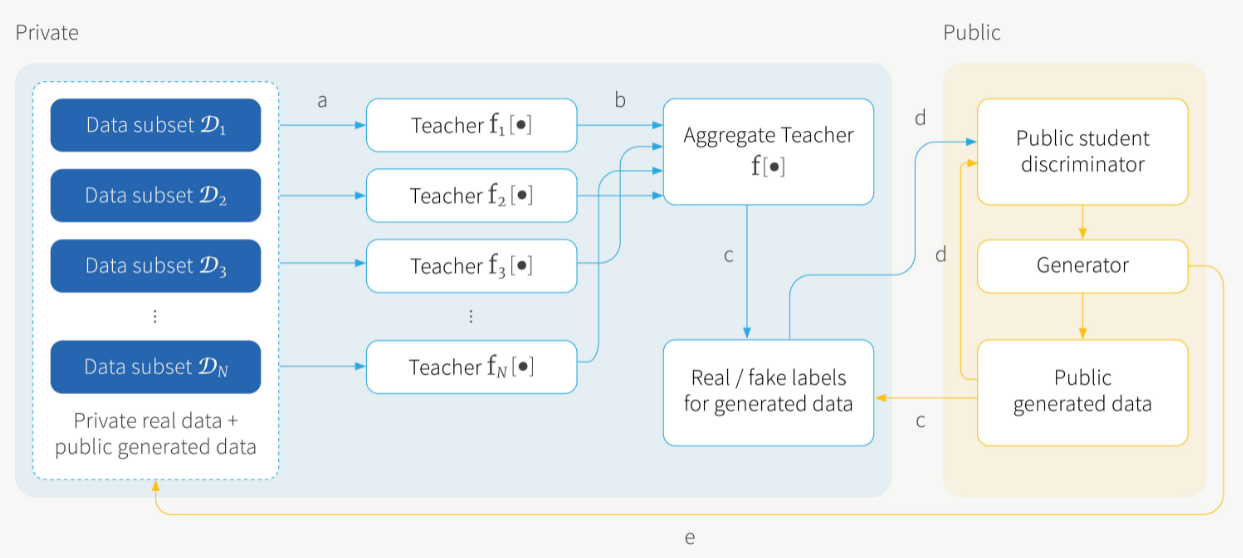
PATE-GAN的训练过程
- 基于真实隐私样本以及生成器生成样本训练教师集合
- 各个教师模型结果聚合并加入噪声
- 教师集合对生成器生成的数据加入标签
- 学生模型基于生成器生成的样本以及教师模型的噪声标签训练
- 生成器基于学生模型的输出训练
生成器
PATE-GAN生成器G与标准的GAN框架中一样。形式上它是一个函数\(G\left(\cdot ;\theta_G\right):[0,1]\to U\),含有\(\theta_G\)参数,以随机噪声\(z\sim Unif(\left[0,1\right])\)作为输入,并输出向量\(U=X\times Y,P_G\)表示G在U上产生的分布。生成器将接受训练,以尽量减少其生成样本在学生判别器的损失。给定n个i.i.d样本\(Unif([0,1]),z_1,…,z_n\),给定\(S\)则关于参数\(\theta\)的生成器G的经验误差定义为: \(L_G(\theta_G;S)=\sum_{j=1}^{n}{log(1-S(G(z_j;\theta_G))}\)
教师判别器
形式上,教师判别器(简称为教师)是函数\(T\left(\cdot;\theta_T^1\right),\ldots,T\left(\cdot;\theta_T^k\right):U\rightarrow[0,1]\),每个都包含参数\(\theta_T^i\)。教师们可以从他们相应的数据集分区中得到一个真实的样本。(也就是\(T_i\)可以接收来自\(D_i\)的样本)作为输入或来自生成器的样本。然后训练教师对这些样本进行分类。给定n个\(i.i.d\),\(Unif([0,\ 1]d),z_1,...,z_n\)的样本,对于给定G定义了权值为\(\theta_T^i\)的教师i的经验损失为: \(L_T^i\left(\theta_T^i\right)=-\left[\sum_{u\in{D_i}}{logT_i\left(u;\theta_T^i\right)+\sum_{j=1}^{n}log\left(1-T_i\left(G(z_j;\theta_T^i\right)\right)}\right]\) 每个教师的训练方式与标准GAN框架中判别器训练的方式相同,除了在这里老师只看到对应的它的真实数据的分区。
学生判别器
标准学生模型提供的差分隐私保证仅针对原始数据D,而不是用于训练学生的公开数据P。在PATE-GAN中,由于没有公开的数据,整个重点都是生成合成数据,因此提出一种新的方法来在没有公开数据的情况下训练学生。 PATE框架中描述的学生训练范式将使用近似于训练生成器的数据来训练学生,也就是从每种样本中获取相同数量的样本,然后使用标准\({PATE}_\lambda\)机制标记这些样本(此处“标记”是指为它们分配一个真/假标签),此处只考虑训练学生对教师标签生成的样本的影响。 在训练生成器时,仅根据生成器生成的样本对判别器进行评估,而不是真实的数据,可以理解为训练生成器使其在所需分布上表现良好。但是,如果学生仅从生成器中看到非真实的样本(即大多数教师将其标记为假的生成样本),相当于学生得不到可用于改善生成器生成样本质量的信息。因此重要的是训练学生的一些生成的样本的标记是真实的。
如果\(Supp(P_U)\subset Supp(P_G)\),那么一些生成的样本将是真实的。为了保证\(Supp(P_U)\subset Supp(P_G)\),将数据归一化为\([0,1]\),然后使用Xavier初始化随机初始化生成器的参数。由此可推出当\(Z\sim Unif(\left[0,1\right]^d),Supp\left(P_U\right)\subset\left[0,1\right]^d\subset G\left(\left[0,1\right]^d\right)=G\left(Supp\left(Z\right)\right)=Supp\left(G(Z)\right)\)
使用n个i.i.d,\(Unif(\left[0,1\right]^d),\ z_1,\ ...,\ z_n\)的样本作为学生的训练数据,并使用生成器生成n个样本,\({\hat{u}}_1,\ldots,{\hat{u}}_n\)其中\({\hat{u}}_j=G(z_j)\),并且使用教师用\({PATE}_\lambda\)机制给这些样本加上标签,令\(r_j={PATE}_\lambda({\hat{u}}_j)\)。然后训练学生\(S\left(\cdot;\theta_S\right):U\rightarrow[0,1]\),来最大限度地增大教师标签数据的标准交叉熵损失,即 \(L_S\left(\theta_S\right)=\sum_{j=1}^{n}{r_jlogS\left({\hat{u}}_j,\theta_S\right)}+(1-r_j)\log(1-S\left({\hat{u}}_j,\theta_S\right))\) 对于固定\(\lambda\),更多的教师会导致教师标签的数据集更少的噪声——所增加的噪音比\(n_j\)的噪音要小。这就引入了一种权衡——教师数量少,噪声可能太大,从而使输出毫无意义;教师数量多,用来训练每个教师的数据少,这也可能使输出变得毫无意义,即使噪声的影响小。在这个问题中找到正确的平衡是关键。虽然一个教师的效用可能很低,但通过聚合,甚至是含有噪声的聚合,所得到的分类器实际上具有很高的效用。任何单个样本对输出的影响都很小(因为在更多的教师,每个样本最多只能影响一名教师),这意味着此处差分隐私保证更严格——如果使用更少的教师,该机制仍然假设,在最坏的情况下,一个样本的存在(或缺失)可以完全改变教师的投票,因此仍然需要添加一定的噪音。
为了计算算法的隐私成本,使用矩估计法(moments accountant)来推导出一个依赖数据的隐私保证。\(\alpha(l)\)表示PATE-GAN矩统计,当教师达成更强的共识时,将较低的隐私成本归因于教师的噪声集合,直觉是,当教师达成强烈共识时,单个教师(同样对应单个样本)的影响要低得多,在在投票输出上比(\(n_0\)和\(n_1\))接近时要高。具体推导参考论文。
PATE-GAN的算法

PATE-ACGAN模型
PATE-ACGAN结合了PATE框架以及ACGAN框架,使用ACGAN作为生成器模型、教师模型和学生模型,将类别标签代入到训练的过程,基本思想和方法与PATE-GAN类似。
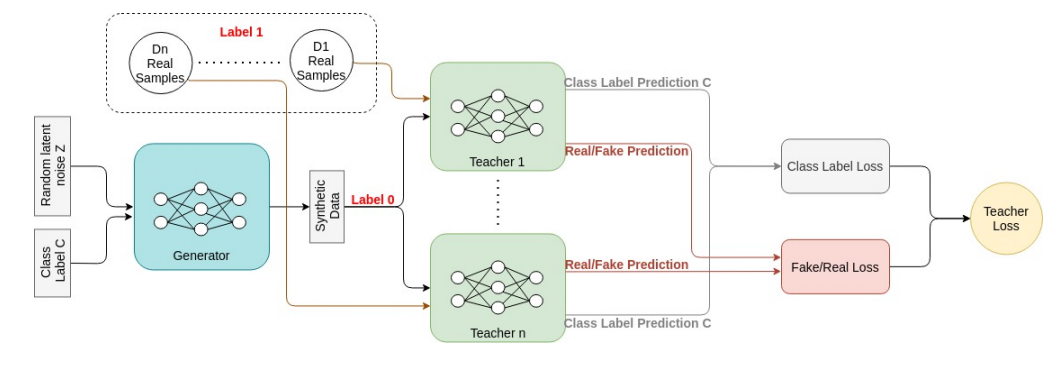
在ACGAN中,生成器得到一个类标签C和一个噪声向量;给定真实数据集的类比,将生成类标签C。然后,给定潜在噪声空间和类标签,生成器的输出将是合成数据。在PATE-ACGAN中设置N个教师判别器,给定生成的数据,将数据预测的类标签,以及输入数据是假的(来自生成器)还是真实的。根据教师们的预测,使用二进制交叉熵来计算教师的损失。每个老师的损失是类标签损失和真实/假损失的总和。直到此步骤如上图所示。教师鉴别器试图将分类损失降到最低,在此步骤中只更新教师的参数。
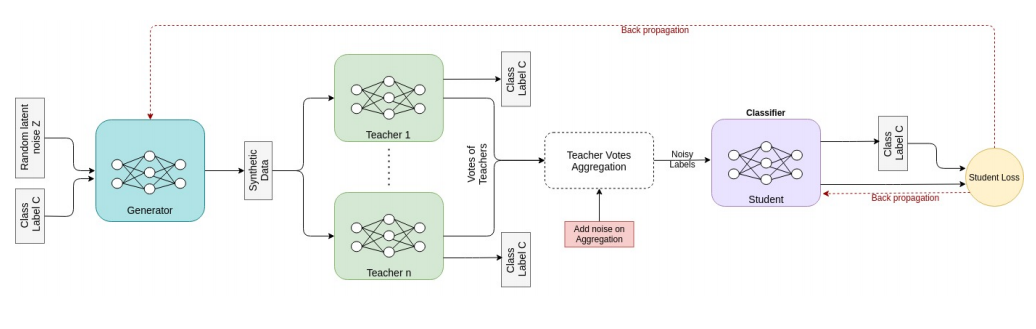
在方法接下来的步骤,与PATE-GAN类似,学生判别器使用带有教师加噪声标记的生成样本进行训练(此处噪声提供了差分保证),学生将使用ACGAN结构。与教师一致,学生的输出是类别和真/假的预测。学生在这个有噪声标记的数据集上最小化分类损失,生成器则训练以最大限度地减少学生的损失。值得注意的是,在这个步骤中没有更新,只有学生和生成器。该训练过程如上图所示。
PATE-ACGAN采用与PATE-GAN相同的隐私保护方法,其中学生判别器无法访问真实的数据集,只受到教师含有噪声的投票结果的影响。因此,这种方法能够保证生成满足差分隐私的数据集,因此可以不加证明的说明PATE-ACGAN可满足与PATE-GAN一致的隐私保障。