机器学习的快速应用增加了人们对在敏感数据(如医疗记录或其他个人信息)上训练的机器学习模型的隐私影响的担忧。为了解决这些这些问题,一个可能的方法为Private Aggregation of Teacher Ensembles,或称PATE,教师集合隐私聚合,它将“教师”模型集合的知识转移到“学生模型”,通过在无交集的数据上分别训练教师来提供直观的隐私保障,并通过对教师的回答进行加噪聚合来提供强大的隐私保证。

本篇教程将基于以下论文进行讲解,主要参考论文[1]和[2]
[1] “Semi-supervised Knowledge Transfer for Deep Learning from Private Training Data”ICLR 2017 best paper
[2] “Scalable Private Learning with PATE” 2018
[3] “MixMatch: A Holistic Approach to Semi-Supervised Learning” 2019
[4] “Private-kNN: Practical Differential Privacy for Computer Vision” 2020
[5] “Antipodes of Label Differential Privacy: PATE and ALIBI” 2021
本篇报告内容主要包括:
- PATE框架
-
PATE的聚合机制
- 基于Lapace加噪机制的LNMax
- 基于高斯加噪机制的GNMax
- 改进:Confident-GNMax聚合机制
- 改进:Interactive-GNMax聚合机制
- 隐私成本分析
- PATE框架下的半监督学习探讨
- 实验方法和结果分析
- 基于开源代码讲解PATE的具体实现
本文内容由本人整理分析,未经作者同意禁止转载。
简介
背景
一些具有巨大益处的机器学习应用只有通过分析敏感数据,如用户的个人联系人、私人照片或通信,甚至医疗记录或遗传序列,才能发挥作用。理想情况下,在这些情形中,学习算法将保护用户训练数据的隐私,例如,通过保证基于隐私数据训练获得的模型不包含任何个体用户的细节。但是,已建立的算法没有提出这类的保证。虽然最先进的算法能够很好地推广到测试集,但在某种意义上它们持续地过拟合特定的训练样本,因此隐私训练数据在这个过程中是被模型隐式记忆的。
利用机器学习中隐式记忆的特性进行的攻击表明,从模型恢复隐私敏感的训练数据细节的可能性,如下图所示的攻击类型,在获取模型的黑盒访问权限的情况下,模型反演攻击(Model Inversion Attack)主要是利用机器学习系统提供的一些API来获取模型的初步信息,并通过这些初步信息对模型进行逆向分析,获取模型内部的一些隐私数据的统计信息;成员推理攻击(membership attack)能够通过模型输出推理某条数据是否存在于训练集。

进一步考虑对模型进行白盒攻击,Zhang et al. (2017)在”Understanding deep learning requires rethinking generalization”表明机器学习模型有能力记住训练数据,通过对模型参数和输出进行分析也能够泄露训练数据的隐私。基于这些考虑Papernot et al., 2017提出了对于训练数据的隐私保证必须适用于最坏的情况,也就是说需要谨慎地假设攻击者可以不受限制地访问模型,即攻击时,攻击者知道模型的一切细节,包括参数、结构等等。

因此这里PATE的研究假设的Threat Model为:能够进行不限次数查询并且能够访问模型内部参数的对手。
1.2 目标
为了使得高效用的机器学习模型与对敏感训练数据的隐私保护保证兼容,教师集合隐私聚合(Private Aggregation of Teacher Ensembles,PATE)方法被提出,PATE的优点是能够从独立的 “教师 “模型的聚合共识中学习,这些模型在无交集的数据上训练,既能提供直观的隐私保证,又与底层机器学习技术无关。在PATE方法中,多个教师在不相干的敏感数据(例如,不同用户的数据)上接受训练,并以黑箱方式使用教师的汇总共识答案来监督 “学生 “模型的训练。通过只公布学生模型(保持教师的隐私),并将噪声添加到用于训练学生的聚合回答中,建立了严格的差分隐私保证。
总的来说,PATE解决的问题是训练分类器时保护训练数据隐私,并且其设计主要具有以下目标:
- 具备隐私黄金标准——差分隐私保护的保证
- 直观上的隐私保证(参考2.2中聚合机制的分析)
- 一般性:模型的学习策略和隐私分析并不取决于用于训练教师或其学生的机器学习技术的细节。
1.3 与DP-SGD的异同
之前专题中介绍的深度学习中满足差分隐私要求的DP-SGD算法,通过在训练过程中对梯度进行裁剪并添加高斯噪声,保证训练过程的差分隐私性质,同样具备防范可以进行不限次数查询并且能够访问模型内部参数的对手的能力。
相比之下PATE主要的贡献在于提出了一个新的学习场景,即半监督学习,使得模型在学习过程中能够利用公开的无标注的数据集,在满足差分隐私约束的条件下利用知识迁移的方式获取带有伪标签的数据,从而基于部分标注数据和部分无标注数据进行训练;同时,PATE与具体学习算法独立,而DP-SGD则特定于基于随机梯度下降训练的模型;以及PATE的噪声添加在教师集合的输出上,也就是模型的输出的结果,而DP-SGD的噪声加在模型训练过程中的梯度上。
PATE框架
为了在学习过程中保护训练数据的隐私,PATE将知识从在数据分区上训练的教师模型集合转移到学生模型中,可以提供直观隐私保证,并通过差分隐私的方式进行表达。如下图所示,PATE框架由三个关键部分组成(1) 由n个教师模型组成的集合(2) 聚合机制(3) 学生模型
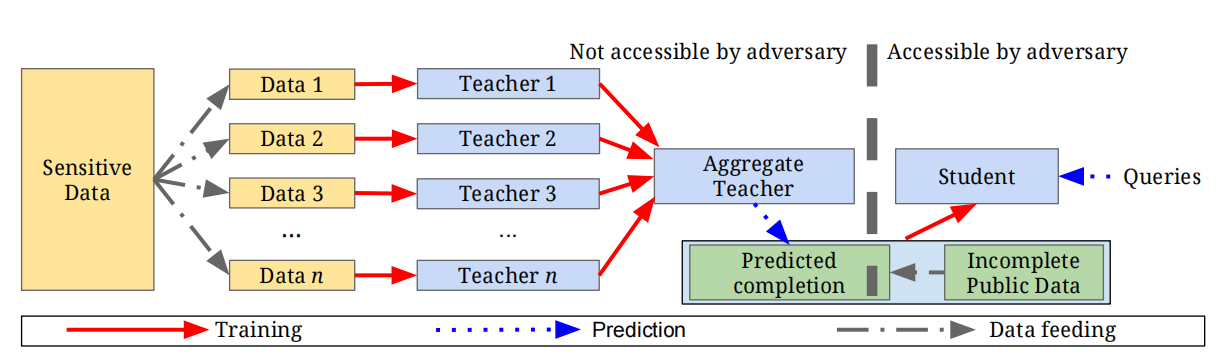
教师模型
训练教师模型集合是整个训练过程的开端,重复利用同一部分数据会增强隐私泄露的风险,出于隐私保护的考虑,在划分原始数据集时做出了disjoint的约束,也就是说原始的隐私数据中的一条数据只可能出现在某一个partition中,每个教师都在对应数据子集上独立训练的模型,即确保了没有一对教师会在重叠的数据上进行训练。
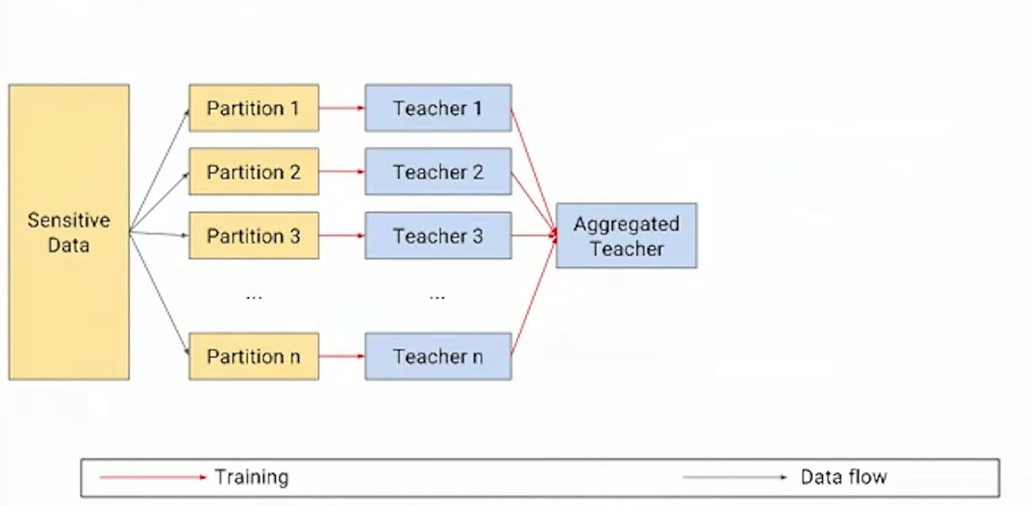
教师模型主要分为两个阶段:
数据分区和训练教师模型:数据集$(X,Y)$,其中$X$表示输入的集合,$Y$表示标签的集合,将数据划分为$n$个不相交的集合,并分别在每个集合上训练模型,由此获得了$n$个称为教师的分类器,接着将训练完成的教师模型部署为一个集合。
结果聚合:在预测阶段的时候,通过查询,每个老师对输入$x$分别进行预测,并将它们聚合成一个单一的预测\(n_{i}(x) \triangleq\mid j:f_{j}(x)=i\mid\),即对教师集合分配给每个类的票数进行统计,令$m$作为任务中的类的数量,给定类$j\in [m]$和输入来计算 分类为\(j\)的教师数量的标签计数。
聚合机制
得到教师集合的标签计数之后,如果简单的将计数中数量最多的类作为预测结果,集合的结果可能取决于一个教师,比如在某次基于教师集合的预测中,当两个类获得票数最多相差一的时候,如果一个老师做出了不同的预测,预测的输出就可能出现变化,因此为了严格保证差分隐私,PATE框架的聚合机制对分配给每个类的票数进行统计,将噪声添加到所得的投票直方图中,并输出加噪后具有最多票数的类作为集合预测的结果, 根据加入噪声类型的不同可以分为两种加噪机制:一个是基于Laplace噪声的机制,被称为max-of-Laplacian,或称 LNMax;另一是基于高斯噪声的机制,被称为max-of-Gaussian,或称GNMax,将在第3节的PATE聚合机制中进一步介绍。
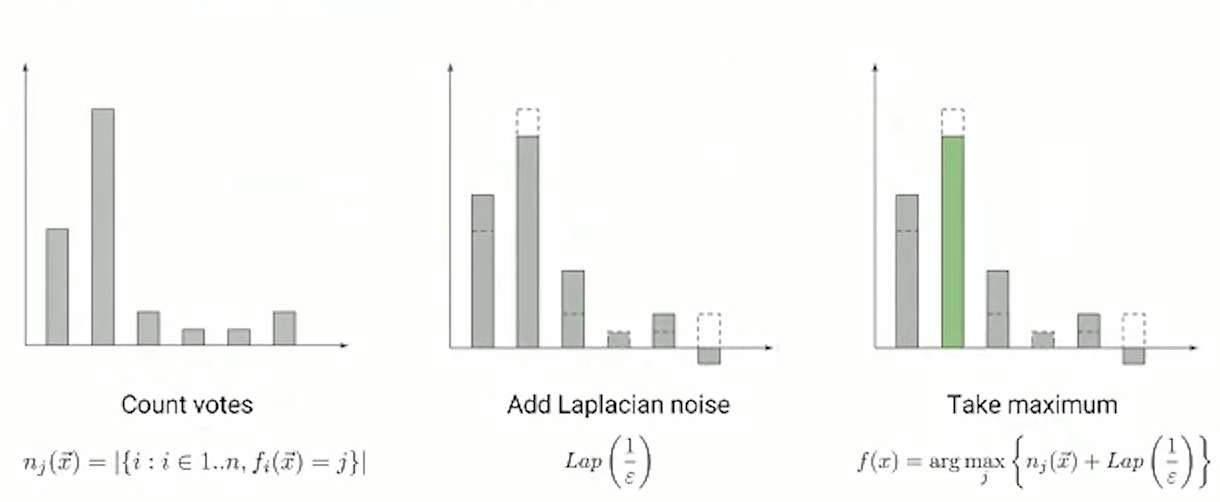
直观的隐私保证的解释:当教师之间有强烈的共识时,他们多数同意的标签并不取决于任何特定教师模型,这时对于任何给定的训练数据点来说具有直观上的隐私保证,如下图为两个教师投票直方图:
- 对于左图可以观察到大部分的教师都达成了共识,因此如果原始隐私数据集中的某个数据发生改变,最多仅改变一个partition上一个教师的结果,由于这里教师们达成了强烈的共识,一个特定partition上的改变不会影响最终的结果,因此这种情形下的隐私成本很小
- 而对于右图,教师集合的输出在三个类上的结果都非常相近,可以得知这里的教师集合没有达成强烈的共识,当原始数据集中的某一个数据点改变,就会可能影响对应分区上的教师的结果,从而改变最终的结果,因此在教师集合在某些类存在接近票数的情况下隐私成本较大。
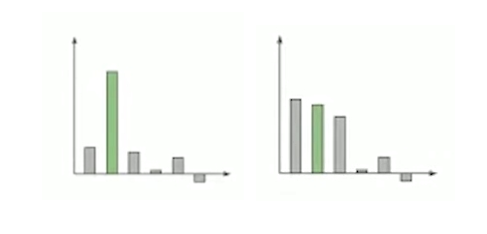
这里就需要关注一个问题,教师的数量是如何影响这里的隐私成本的?基于教师集合投票直方图进行加噪的结果,为了确保所获得的的结果是正确的,噪声的尺度应该比结果中两个最大的\(n_j\)的差值要小,利用差分隐私的噪声机制相关定理可以证明隐私成本越小对应的噪声尺度越大,因此一般情况下,数值间较大的差距会转化成较小的隐私成本。由于差距本身随着教师数量的增加而增加,因此更多的教师会降低隐私的成本。但是如果隐私数据的数量是固定的,比如在一般的现实场景下,隐私数据对应的是某些公司机构中一定数量的数据,在有\(n\)个教师的情况下,每个教师只在\(\frac{1}{n}\)的数据子集上面训练,对于足够大的\(n\),每个教师的训练数据将会太少,以至于教师本身的性能变差,从而影响整体性能,因此可以看出在整体模型表现以及隐私成本这里有一个基于教师数量多少的权衡。
这里还需要注意的是,如果单纯依靠加噪后的教师集合\(f\)进行预测输出会带来几方面的问题:在限制隐私成本的情况下,首先随着预测数量的增加,隐私成本不断被消耗,隐私成本减少同步导致往结果中加入的噪声也会增加,从而使得经过很多轮查询后所获得的回答无效;其次,如果当攻击者有权访问模型参数时,也就是背景部分提及的白盒攻击的场景下,由于每位教师\(f_i\)训练的时候都没有考虑隐私问题,这些教师本身可能会泄露模型细节,因此隐私保证不存在。为了解决这些限制,PATE使用教师集合预测的固定数量的标签来训练另一种模型,即学生。
学生模型
PATE的最后一步是通过使用公共但未标记的数据从教师集合中转移知识来训练学生模型。根据的分析,归纳训练学生模型的必要性主要有以下两点:
- 教师集合的每一次预测都增加了整体的隐私损失,隐私成本限制了查询数量以及准确性
- 对于教师集合模型内部的检测可能会揭露隐私数据,这对应于前面提到的隐私保证需要去防范白盒攻击
因此为了限制标注的隐私成本,只对公共数据的子集采用聚合机制进行查询,作者提出了以半监督的方式和固定数量的查询来训练学生;固定的查询固定了隐私成本也能够减少分析模型参数来恢复训练数据的攻击可能性,因为学生只能接触到公共数据和具有隐私保护保证的标签。
目前有许多技术可以进行知识迁移,从而降低学习过程中学生对老师集合的查询,包括:蒸馏、主动学习、半监督学习。其中较为有效的技术是将生成对抗网络(GANs)应用于半监督学习。
[1]Papernot et al., 2017提出的PATE-G模型为用GANs进行半监督学习,用到了improved GANs(2016)这个模型;[2]Papernot et al., 2018使用的是性能更好的虚拟对抗训练virtual adversarial training(VAT)。以下对生成对抗网络(GANs)应用于半监督学习的方法进行简要的介绍,更多细节可参考对应论文。
基于GANs的半监督学习
在传统的GAN中,判别器被训练来判断给定图像是真的(来自数据集)还是假的(由生成模型生成),甚至在无标签的情况下,使其能够从图像中学习用来判别的特征,从这种意义上讲,判别器类似于特征提取器。尽管GANs的用处大多在于用其中的生成器来生成接近真实图像的数据,但是由于判别器已经学习训练数据中的图像特征,因此能够产生较好的分类性能,因此判别器在这里也可以作为迁移学习的起始点,基于数据集训练一个分类器,使监督学习能够从无监督学习中受益。
半监督场景下GANs的判别器同时在两种模式下被训练:无监督和有监督。在无监督状态下,就像在传统的GAN中那样,判别器需要区分真实图像和生成的图像;在有监督的情况下,像在一个标准的神经网络分类器中一样,鉴别器需要把图像正确分类。
为了同时训练这两种模式,判别器必须输出1+n个节点的值,其中1代表 “真假 “节点,n是分类任务中的类别数。这涉及到同时为无监督的GAN任务和有监督的分类任务直接训练判别器模型。
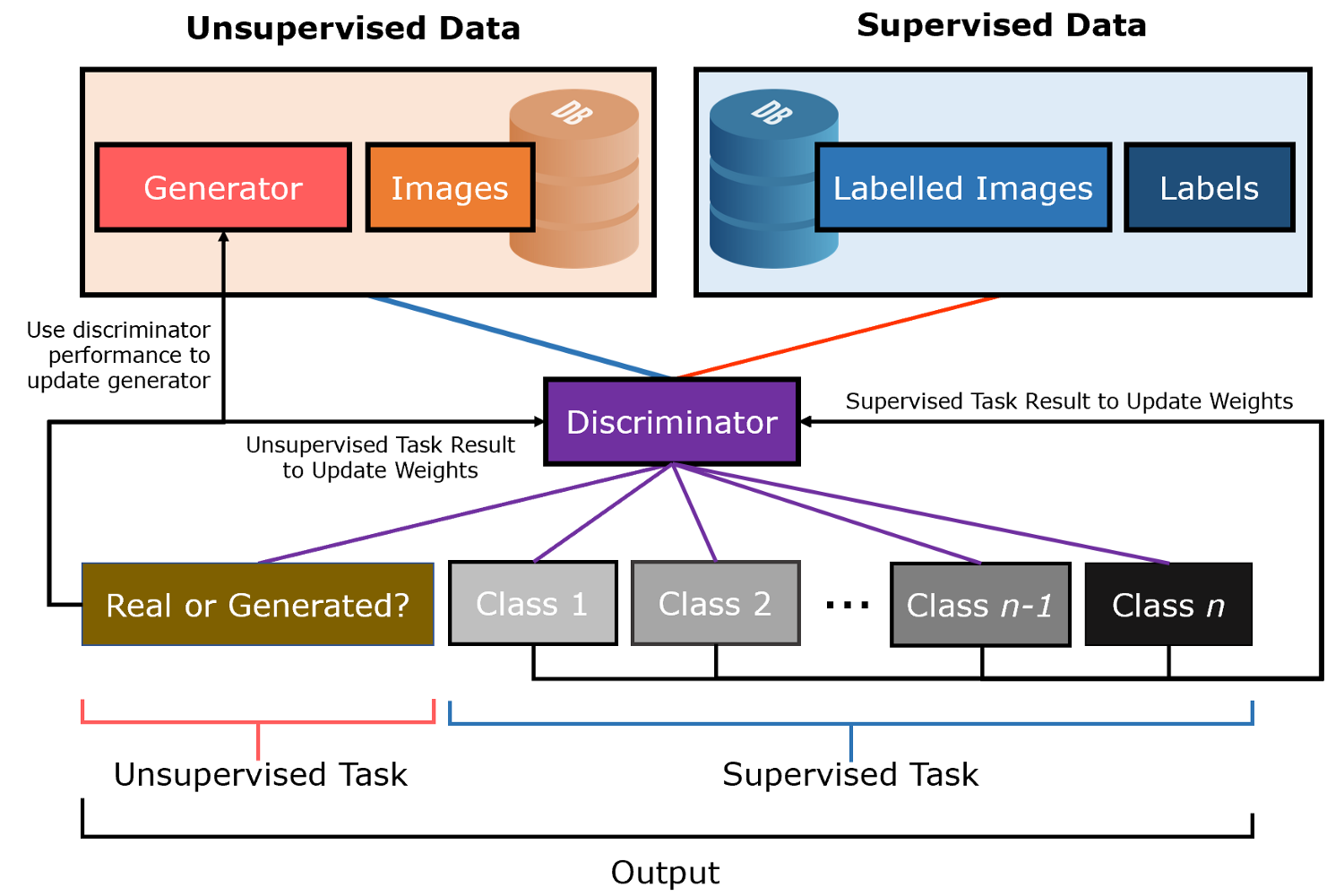
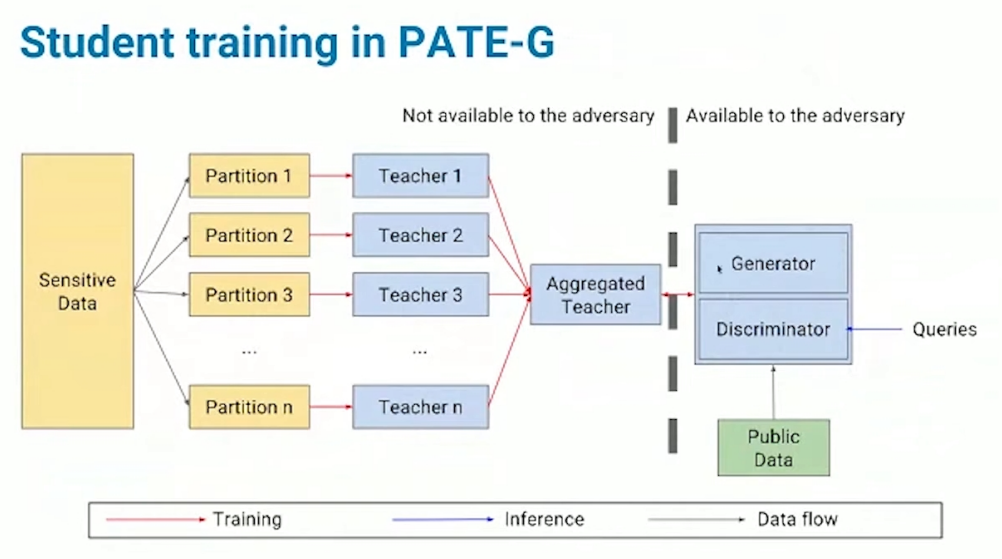
PATE-G
在训练的时候,PATE-G的数据类型可以分为3类:(1)少量有标注的数据集(2)无标注的数据集(3)生成器生成的数据集;PATE机制对半监督GANs的训练的贡献在于提供少量的有标注数据集,此时生成器和判别器同时进行训练优化;当对学生模型进行查询操作的时候,仅对具有分类功能的判别器部分进行查询。
聚合机制及其隐私分析
聚合步骤是PATE的一个重要组成部分。它能够实现从教师到学生的知识转移,同时提供隐私保证,PATE方法将传统的Private Learning(DP-SGD)在学习阶段提供隐私保护的方式转到了聚合的阶段,以下将详细分析PATE的两种聚合机制及其所提供的隐私保证。
PATE聚合机制的框架:对于样本\(x\)和类\(1, . . . ,m\),令\(f_j(x)∈[m]\)表示第j个教师模型的预测,\(n_i\)表示第\(i\)类的投票数(即\(n_{i} \triangleq \mid f_{j}(x)=i\mid\) )。加噪机制的输出是\(\mathcal{A}(x)\triangleq argmax_i (n_i(x) + Noise)\) 。通过对这一机制的严格分析,PATE框架提供了一个差分隐私API:教师集合所做的每个聚合预测的隐私成本是已知的。
定义1. (隐私损失)令\(\mathcal{M}:\mathcal{D}\to\mathcal{R}\)为一个随机机制,\(d\),\(d'\)是一对相邻的数据库,令\(\operatorname{aux}\)表示辅助输入。对于一个结果\(o\in R\),在\(o\)处的隐私损失被定义为 \(c\left(o ; \mathcal{M}, \operatorname{aux}, d, d^{\prime}\right) \triangleq \log \frac{\operatorname{Pr}[\mathcal{M}(\operatorname{aux}, d)=o]}{\operatorname{Pr}\left[\mathcal{M}\left(\operatorname{aux}, d^{\prime}\right)=o\right]}\) \(c\left(\mathcal{M}, \operatorname{aux}, d, d^{\prime}\right)\)对应的隐私损失随机变量定义为\(C\left( \mathcal{M}(d); \mathcal{M}, \operatorname{aux}, d, d^{\prime}\right)\),即通过评估从\(\mathcal{M}(d)\)采样的结果的隐私损失定义的随机变量。随机机制\(\mathcal{M}\)在这里就指代添加随机噪声的NoisyMax机制,辅助输入\(\operatorname{aux}\)在DP-SGD训练过程对应中第\(t\)次迭代,由\(t-1\)次所获得的参数\(\theta_{t-1}\),而在PATE的NoisyMax机制里\(\operatorname{aux}\)对应学生模型可以获得的公开数据集。
LNMax Aggregator
首先介绍的是[1](Papernot et al., 2017)中的Laplacian NoisyMax(LNMax);记位置参数为0,尺度参数为的$b$的Laplace分布为$Lap(b)$,其概率密度函数为\(p(x)=\frac{1}{2 b} \exp \left(-\frac{\mid x\mid}{b}\right)\)。
定义2. (Laplacian NoisyMax机制) 对于样本\(x\)和类\(1, . . . ,m\),令\(f_j(x)∈[m]\)表示第j个教师模型的预测,\(n_i\)表示第\(i\)类的投票数(即 \(\vec{x}: n_{j}(\vec{x})=\mid\{i: i \in[n]\}, f_{i}(\vec{x})=j\mid\))。Laplacian NoisyMax(LNMax)聚合机制定义为: \(\mathcal{M}_γ(x)\triangleq argmax_i \{n_i(x) + \operatorname{Lap}\left(\frac{1}{\gamma}\right)\}\) 对于LNMax聚合机制的隐私分析主要是利用矩会计(moments accountant)隐私分析框架进行,分别基于(Papernot et al., 2017)工作中提到的无数据依赖的隐私分析和有数据依赖的隐私分析进行介绍。
\[n_{i}(x) \triangleq\left|j:f_{j}(x)=i\right|\] \[n_{i} \triangleq\left|f_{j}(x)=i\right|\] \[\vec{x}: n_{j}(\vec{x})=\left|\{i: i \in[n]\}, f_{i}(\vec{x})=j\right|\] \[p(x)=\frac{1}{2 b} \exp \left(-\frac{|x|}{b}\right)\]无数据依赖的隐私分析
约束隐私损失的一个自然的方法就是先约束学生查询每个标签的隐私成本,然后使用强组成定理来推导出训练学生的总成本。考虑这种情形,对于相邻的数据库$d$,$d’$,每个教师得到相同的训练数据分区(也就是说,$d$和$d’$对应同样的老师),其中只有一个老师的训练数据分区不同。因此对于任何样本$\vec{x}$,在$d$和$d’$上的投票计数最多只在两个地方相差1。
基于矩会计的数据隐私分析流程(Papernot et al., 2017):利用下面的定理1可以计算给定噪声尺度下的矩会计的上界,基于几个\(l\)的值(最大为8的整数值)计算矩会计$α$的值。根据矩会计的组成性,能够去累计连续的步骤中的这些界的综合,并结合矩会计的尾界从最终的$α$推导出$(ε,δ)$差分隐私保证。
定理1. 假设在相邻的数据集$d$,$d’$上,标签计数\(n_j\)在每一维上最多相差1。令\(\mathcal{M}\)为\(\mathcal{M}(x)\triangleq argmax_i \{n_i(x) + \operatorname{Lap}\left(\frac{1}{\gamma}\right)\}\)即定义4中的Laplacian NoisyMax机制。则\(\mathcal{M}\)满足$(2γ, 0)$-差分隐私。此外,对于任意$l$,\(\operatorname{aux}\),$d$和$d’$: \(\alpha(l;\operatorname{aux},d,d')\le2\gamma^2l(l+1)\) 即在每一步查询,使用噪声\(Lap( \frac{1}{γ} )\)的聚合机制,满足\((2γ, 0)\)-DP。推导可得出经过\(T\)个查询之后,可以推导获得\(\left(4 T \gamma^{2}+2 \gamma \sqrt{2 T \ln \frac{1}{\delta}}, \delta\right)\)差分隐私,但是这个界可能非常大,因此作者介绍了通过依赖于原始数据分布的隐私分析方法,及其降低隐私成本界的有效性。
数据依赖的隐私分析
数据依赖即根据原始数据集的一些分布特征进行进一步的隐私分析,这能够大大降低隐私的界;这里的隐私分析利用了这样一个事实:当教师的集合的人数非常多的时候,多数的投票结果具有压倒性的可能性,在这种情况下,隐私成本就很小。这里同样基于矩会计的方法,在统一的框架流程进行分析,下面的定理为差分隐私机制的矩估计提供了一个与数据相关的约束。
定理2. 令\(\mathcal{M}\)满足\((2γ, 0)\)-差分隐私并且对于一些输出\(o^*\) 有\(q\ge Pr[\mathcal{M}(d)\ne o^*]\)令\(l,\gamma\ge0\)并且\(q<\frac{e^{2\gamma}-1}{e^{4\gamma}-1}\),则对于任意aux 以及任意相邻数据集$d$和$d’$,\(\mathcal{M}\)满足: \(\alpha\left(l ; \operatorname{aux}, d, d^{\prime}\right) \leq \log \left((1-q)\left(\frac{1-q}{1-e^{2 \gamma} q}\right)^{l}+q \exp (2 \gamma l)\right)\) 同时使用下面定理对该聚合机制的参数\(q\)进行上界的约束
定理 3. 设\(n\)是基于数据集\(d\)的标签的投票数向量,对所有\(j\)来说,\(n_{j^∗}\ge n_j\),即\(j^∗\)表示原始投票数向量中具有最多票数的类,满足: \(\operatorname{Pr}\left[\mathcal{M}(d) \neq j^{*}\right] \leq \sum_{j \neq j^{*}} \frac{2+\gamma\left(n_{j^{*}}-n_{j}\right)}{4 \exp \left(\gamma\left(n_{j^{*}}-n_{j}\right)\right)}\) 这使我们能够基于教师集合投票的分数向量$n$对$q$进行一个上界的约束,从而对于特定的矩估计的值\(\alpha\)进行限界,这里使用定理1和定理2中较小的界。
对比前面无数据依赖的隐私分析所获得的的隐私界和有数据依赖的所获得的的隐私界:如果将该计算应用于(Papernot et al., 2017)在SVHN实验上,设置以下参数值γ=0.05,T=1000,δ=1e-6,得到无数据依赖隐私成本ε≈26,数据依赖隐私成本ε≈8.19 ,或者应用MNIST实验上,设置以下参数值γ=0.05,T=100,δ=1e-5,得到无数据依赖隐私成本ε≈5.80,数据依赖隐私成本ε≈2.04。可以看到数据依赖的方法显著地降低了隐私成本。
这里还需要注意到的一点是,由于这里隐私矩估计(privacy moments)本身是依赖数据的,所以最终$ε$也是依赖于数据的,不应该被公开。为了解决这个问题,可以对矩估计的平滑敏感度进行限界,并将与之成比例的噪声添加到矩估计本身,从而实现满足差分隐私的隐私成本估计。在(Papernot et al., 2017)LNMax的验证工作中直接将这部分略去,而在接下来介绍的GNMax(Papernot et al., 2018)重新对于这部分的平滑敏感度进行设计应用和分析。
GNMax Aggregator
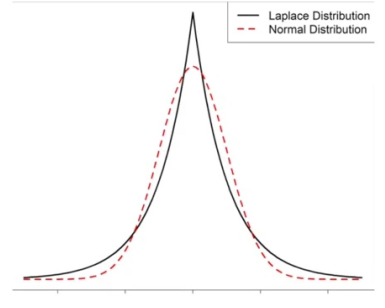
Gaussian NoisyMax(GNMax)是(Papernot et al., 2018)中提出的利用高斯噪声对于教师投票结果进行加噪聚合的机制,高斯分布比LNMax使用的拉普拉斯分布更加集中,当类的数量$m$很大时,这种集中的性质直接提高了聚合的效用,以下介绍的是高斯机制的定义以及GNMax机制的定义,其中$\mathcal{N}(0,\sigma^2)$为均值为$0$,方差为$\sigma^2$的高斯分布,对应于差分隐私中的高斯机制,所提供的是松弛的差分隐私保证。
定义3. Gaussian NoisyMax(GNMax)机制 对于样本$x$和类$1, . . . ,m$,令$f_j(x)∈[m]$表示第j个教师模型的预测,$n_i$表示第$i$类的投票数(即$n_{i}(x) \triangleq\left|j:f_{j}(x)=i\right|$)。将Gaussian NoisyMax(GNMax)聚合机制定义为: \(\mathcal{M}_\sigma(x)\triangleq argmax_i \{n_i(x) + \mathcal{N}(0,\sigma^2)\}\)
上面介绍的LNMax聚合机制的隐私分析主要是基于矩会计(moments accountant)隐私分析框架进行,在GNMax方法进行隐私分析时选择使用Rényi Differential Privacy(RDP)作为一个更自然的分析框架,由于前面已提及无数据依赖的隐私分析将会导致松散的隐私界,因此GNMax(Papernot et al., 2018)的隐私分析工作集中于对数据依赖的隐私分析。
$(ε, δ)$差分隐私和RDP都是对纯$ε$差分隐私的松弛,RDP的两方面主要优势如下:首先,RDP的组合方式很好;其次,与$(ε, δ)$差分隐私相比,RDP以更清晰的方式捕获了高斯噪声的隐私保证,这让我们能够对GNMax机制进行隐私分析,这方面的优势见下面分析。LNMax机制依赖RDP的第一个方面优势,而对于GNMax机制的分析能够同时依赖于这两个方面的优势。
数据依赖的隐私分析
对高斯噪声的聚合机制进行数据依赖性的隐私分析比基于拉普拉斯噪声的LNMax隐私分析更具挑战性,具体细节可以参考(Papernot et al., 2018)论文的证明。然而分析的复杂性增加并没有使算法变得更加复杂,从而能够改善隐私-效用的权衡。
通过平滑的敏感性分析对隐私成本进行去隐私依赖。数据相关的隐私分析的另一个挑战在于现在隐私成本本身是依赖于隐私数据的一个函数,针对这一点,使用(Nissim et al., 2007)提出的平滑敏感性框架,这里的对隐私估计进行脱敏的增量隐私成本是适度。
定理4. 对所有输入和所有$λ≥1$都成立,GNMax机制\(\mathcal{M}_\sigma(x)\triangleq argmax_i \{n_i(x) + \mathcal{N}(0,\sigma^2)\}\)满足$(λ,λ/σ^2)-RDP$。
若是直接应用组合定理宽松的隐私界,一个直观的例子为,若将标准的高级组成定理应用于本文第5节实验部分的表2最后两行的实验,对于Glyph数据集,在$δ=10^{-8}$时,会得到$ε=8.42$和$ε=10.14$,对可以观察到比最终获得的隐私界大很多。因此采用的是数据依赖的隐私分析,实现在相同的$δ$条件下产生小于1的$ε$值。
下面所提出的定理将与数据无关的高阶RDP保证转化为与数据相关的较小阶$λ$的RDP保证。将其与命题10一起使用,使得GNMax算法的每个查询的隐私成本能够作为参数$\tilde{q}$ 的函数进行约束,$\tilde{q}$ 为最多投票的回答不被机制输出的概率(也就是经过加噪后获得的结果是错误的概率)。
定理5. 假设\(\mathcal{M}\)是一个具有\((\mu_1, \varepsilon_1)\)-RDP和\((\mu_2, \varepsilon_2)\)-RDP保证的随机算法,给定一个数据集\(D\)和一个约束\(\tilde{q} \le 1\),并假设存在一个可能的结果\(i^∗\),使\(\tilde{q} \ge Pr[\mathcal{M}(D)\ne i^*]\)。此外,假设\(\lambda \le \mu_1\),\(\tilde{q} \leq e^{\left(\mu_{2}-1\right) \varepsilon_{2} /\left(\frac{\mu_{1}}{\mu_{1}-1} \cdot \frac{\mu_{2}}{\mu_{2}-1}\right)^{\mu_{2}}}\)。那么,对于\(D\)的任何相邻的数据集\(D'\),我们有: \(D_{\lambda}\left(\mathcal{M}(D) \| \mathcal{M}\left(D^{\prime}\right)\right) \leq \frac{1}{\lambda-1} \log \left((1-\tilde{q}) \cdot \boldsymbol{A}\left(\tilde{q}, \mu_{2}, \varepsilon_{2}\right)^{\lambda-1}+\tilde{q} \cdot \boldsymbol{B}\left(\tilde{q}, \mu_{1}, \varepsilon_{1}\right)^{\lambda-1}\right)\) 其中\(\boldsymbol{A}\left(\tilde{q}, \mu_{2}, \varepsilon_{2}\right) \triangleq(1-\tilde{q}) /\left(1-\left(\tilde{q} e^{\varepsilon_{2}}\right)^{\frac{\mu_{2}-1}{\mu_{2}}}\right)\)并且\(\boldsymbol{B}\left(\tilde{q}, \mu_{1}, \varepsilon_{1}\right) \triangleq e^{\varepsilon_{1}} / \tilde{q}^{\frac{1}{\mu_{1}-1}}\)
关于定理5的一个简单版本的描述如下:假设\(\mathcal{M}\)是一个具有\((\mu_1, \varepsilon_1)\)-RDP和\((\mu_2, \varepsilon_2)\)-RDP保证的随机算法,给定一个数据集\(D\)和一个约束\(\tilde{q} \le 1\),并假设存在一个可能的结果\(i^∗\),\(\tilde{q} \ge Pr[\mathcal{M}(D)\ne i^*]\)。那么对于机制\(\mathcal{M}\)在数据集\(D\)上的数据依赖的\(\lambda\)阶的Rényi differential privacy,当\(\tilde{q} \to0\)的时候,将由参数\(\tilde{q} ,\mu_1,\varepsilon_1,\mu_2,\varepsilon_2\)所组成的一个函数作为上界进行约束。
只要算法在对应输入数据集\(D\)上的输出分布有一个强的峰值(即$\tilde{q} \ll 1$),这个约束就会改善基于$λ$的数据无关的隐私界,但是接近1的$\tilde{q}$ 值可能会导致更宽松的约束。在实践中,取定理5的约束和定理4的约束$λ/σ^2$(与数据无关的约束)中的最小值。另外值得注意的一点为定理9包含了3.1.2小节的定理2,即满足$ε$-差分隐私的机制($μ_1=μ_2=∞$,$ε_1=ε_2$)。
下面提出的定理是用来约束当$i^*$对应于具有真正多数的教师投票的类时,聚合器输出结果改变的概率$\tilde{q}$
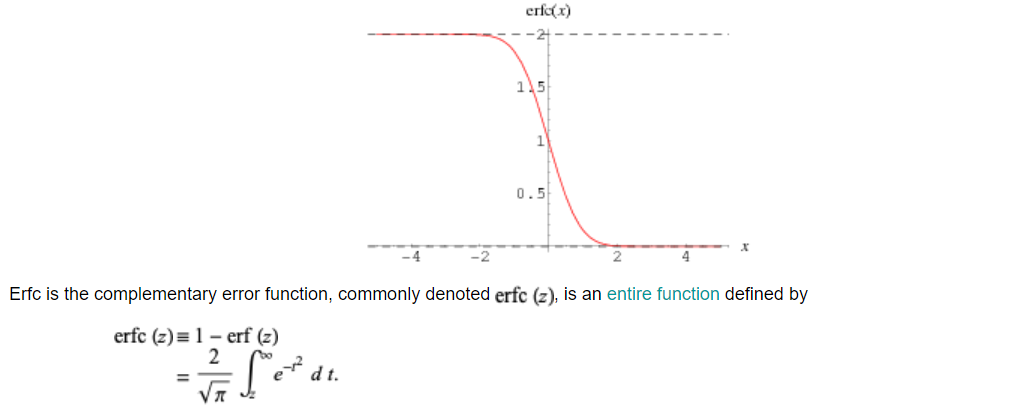
定理6. 对于GNMax聚合器\(\mathcal{M}_\sigma\),教师的投票直方图\(\bar{n} = (n_1, . . . , n_m)\),对于任意\(i^∗∈[m]\),\(Pr[\mathcal{M}_\sigma(D)\ne i^*]\le q(\bar{n})\),其中\(q(\bar{n}) \triangleq \frac{1}{2} \sum_{i \neq i^{*}} \operatorname{erfc}\left(\frac{n_{i^{*}}-n_{i}}{2 \sigma}\right)\),\(erfc\)为complementary error function
complementary error function
可以观察到\(erfc\)关于参数\(z\)是一个单调递减的函数
这些定理的证明可以参考Papernot et al., 2018中的附录部分。简而言之,对于GNMax聚合器的每个查询,给定教师投票$n_i$和具有最多票数的类$i^*$,通过命题6可以获得定理5中使用的$\tilde{q}$ 的值,然后对$μ_1$和$μ_2$进行优化,来获得在一系列阶$λ$下的数据相关的RDP隐私保证。最后使用RDP的组成性质计算获得一连串的查询聚合操作后的RDP,最后将RDP约束转化为$(ε,δ)-DP$约束。
昂贵的查询
这种依赖于数据的隐私分析使得在隐私成本方面得出了昂贵查询的概念。当教师的投票基本上不一致时,基于定理6和erfc函数的单调递减性,一些$n_{i^*} - n_i$的值可能很小,导致$\tilde{q}$ 的值很大:也就是说,教师之间缺乏共识,聚合器很有可能会输出一个错误的标签。因此,从隐私的角度来看,昂贵的查询往往也不利于训练。反之,具有强烈共识的查询能够实现严格的隐私界限。这种协同作用启发了下面几节讨论的聚合机制:它们在回答查询之前评估共识的强度。
Improvement
Improvement对应于Papernot et al., 2018中提出的Confident-GNMax和Interactive-GNMax的聚合器,它们以保护隐私的方式选择值得回答的查询:隐私预算在查询选择和答案计算之间共享。这两个聚合器使用不同的启发式方法来选择查询:前者不考虑学生的预测,而后者则考虑。
Confident-GNMax Aggregator

这里介绍对GNMax聚合器的改进之一,这个改进能够过滤掉那些教师没有足够强的共识的查询。这种过滤方法使教师能够避免回答昂贵的查询,同时这个选择步骤本身是以隐私的方式进行的。
算法1中描述了所提出的高置信的聚合器(Confident-GNMax Aggregator)。为了选择具有压倒性共识的查询,该算法检查最多数的投票是否越过阈值T。为了在这一步中加入隐私保证,结果和阈值的比较是在加入方差为$\sigma^2_1$的高斯噪声之后进行的。然后,对于通过该噪声阈值检查的查询,聚合器以较小的方差$\sigma^2_2$继续进行通常的GNMax机制。对于没有通过噪声阈值检查的查询,聚合器只是简单地返回$⊥$,学生在其训练中丢弃这个样本。
在实践中,经常为$σ_1$选择明显高于$σ_2$的值。选择$T$,是为了让多数得到的票数达不到总数一半的查询(通常非常昂贵)在加入噪声后不可能通过阈值,同时保证在具有强烈共识的查询中仍然有足够高的知识收益,基于这种权衡一般将T值设置为教师数量的0.6倍到0.8倍。
这个聚合器的隐私成本是直观的:为每个查询支付阈值检查隐私成本,同时只为通过检查的查询支付GNMax步骤的隐私成本。在LNMax的工作中,该机制为每个查询支付隐私成本,无论是否昂贵。相比之下,Confident Aggregator在检查阈值时花费的隐私成本要小得多,而且通过回答非常小部分昂贵的查询,使得它总体上花费的隐私成本较低。
Interactive-GNMax Aggregator

这里介绍对GNMax聚合器的第二个改进,虽然自信的聚合器排除了昂贵的查询,但它忽略了学生可能会收到对学习贡献不大的标签的可能性,反过来也忽略了其效用。通过纳入学生当前对其公共训练数据的预测结果的评估,设计了一个交互式聚合器,在学生已经自信地预测了与教师相同的标签的情况下,放弃查询。
给定一组查询,交互式聚合器(算法2)通过比较学生的预测和教师对每个班级的投票来选择那些回答。与自信聚合器的步骤1类似,凡是这些有噪声的差异的数量越过一个阈值的查询,都用GNMax来回答。这个噪声阈值足以强制执行第一步的隐私,因为学生的预测可以被认为是公共信息(学生是以差分隐私的方式训练的)。
对于未能通过这一检查的查询,如果学生有足够的信心,该机制会加强预测的学生标签,并且不需要再次查看教师的投票。这种有限的监督形式是以很小的隐私为代价的。此外,检查的顺序确保了一个对自己的预测有错误信心的学生在与教师的共识不一致的情况下不会被意外地加强。除了考虑教师和学生之间的差异而不是只考虑教师的投票,隐私成本统计与Confident-GNMax Aggregator相同。在实践中,开始时当学生无法做出有效的预测时,可以用Confident-GNMax聚合器训练学生,在学生获得一定的熟练度后,再用Interactive-GNMax Aggregator完成训练。
PATE with Semi-Supervised Learning
之前专题介绍过深度学习中的差分隐私算法,即基于差分隐私的随机梯度下降算法(DP-SGD),在监督学习的场景下,基于隐私数据集训练模型,该算法在模型训练过程中通过梯度裁剪和加入随机噪声进行梯度扰动为模型提供差分隐私保证,然而由于所添加的噪声与模型中参数数量的成正比,使得在合理隐私预算下训练一个大模型非常困难,因此DP-SGD的相关工作局限于轻量级网络架构上。
而PATE提出了一个新的满足差分隐私的机器学习场景,即如论文[1]标题所述的半监督知识迁移“Semi-supervised Knowledge Transfer”,对应于半监督学习。半监督学习的一般场景为基于大量无标注数据,和少量标注数据训练出具备强泛化能力的模型。这个场景非常契合现实中的需求,因为现实中想要获取大量高质量的标注数据往往是一件很困难的事情,需要花费大量的时间和人力成本。
PATE利用在隐私数据的不相干子集上训练的大型教师模型集合,在保证隐私的情况下将知识转移给学生模型,即训练好的教师集合能够通过PATE的聚合机制为公开无标注的数据集的子集打上伪标签,使得学生模型能够在大量无标注的数据和少量有标注的数据的场景下进行半监督学习。
但是正如前面分析中提到的,教师的数量的多少是PATE框架中的一个很重要的参数选择,这个值很大程度上决定了教师集合投票结果中两个最大值之间的差,因此对应了隐私成本的值,一般来说,越多的教师数量,对应的差距会越大,隐私成本越小,根据论文[1]和[2]中展示的结果,通常教师模型的数量需要大到250,才能获得有意义的隐私保证,同时确保足够准确的伪标签;同时当教师模型是一个深度神经网络时,每个模型都需要大规模的数据来实现典型计算机视觉任务的泛化,由于半监督场景下隐私数据相比于公开数据的量很少,因此教师的数量越大,导致一个教师只能够在一个很小的数据分区上面训练,从而严重地影响了教师模型本身的性能,如论文[4]中提到,为CIFAR-10设置教师数量为250时,每个不相干的教师只能够得到200张图像,导致他们的准确率低于50%,从而使得学生模型无法获得有意义的伪标签。 基于这方面的考虑,只有在具备大量的隐私数据数据的情境下,基于PATE的半监督学习才能够达到有效的隐私成本和模型效用良好的权衡。
以下列出几个PATE相关的半监督学习研究:
-
Berthelot, David, Nicholas Carlini, Ian Goodfellow, Nicolas Papernot, Avital Oliver, and Colin Raffel. “Mixmatch: A holistic approach to semi-supervised learning.” arXiv preprint arXiv:1905.02249 (2019).
使用和论文[2]中相同的实验设置,采用新提出的MixMatch半监督方法,实现了隐私成本更小情况下模型性能的提升。具体为:相同任务下,VAT在隐私损失为ε=4.96的情况下达到的91.6%的准确率;MixMatch能够以更小的隐私损失ε=0.97达到95.21±0.17%的测试精度。
-
Zhu, Yuqing, et al. “Private-knn: Practical differential privacy for computer vision.” Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. 2020.
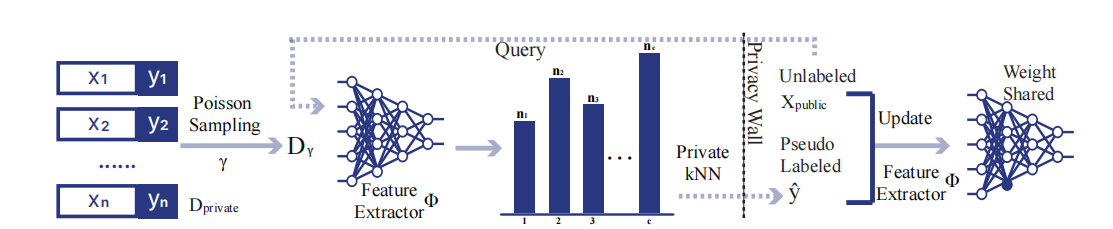
改变了PATE在隐私数据集分割子集上分别训练教师的设定,提出的Private-kNN在隐私数据上训练一个特征提取器,并通过特征空间中的最近邻居对查询进行分类,其中通过对隐私数据的随机subsample能够增加隐私保证
-
Malek Esmaeili, Mani, Ilya Mironov, Karthik Prasad, Igor Shilov, and Florian Tramer. “Antipodes of Label Differential Privacy: PATE and ALIBI.” Advances in Neural Information Processing Systems 34 (2021).
在Label-only的学习场景中,基于PATE框架和GNMax聚合机制利用半监督学习算法FixMatch进行学习,并且提出通过经验性的评估来描述隐私损失。
实验分析
这部分基于Papernot et al., 2017和2018中所展示的实验结果进行分析说明
Papernot et al., 2017
以下为这个工作的实验设置,实验主要在四个公开数据集上进行,不同数据集对应不同的数据集。基于PATE半监督的学习场景,将每个数据集中的测试数据进行划分,取其中一定量的数据作为无标注的公开数据,剩余的数据作为测试训练好的学生模型性能的测试数据。
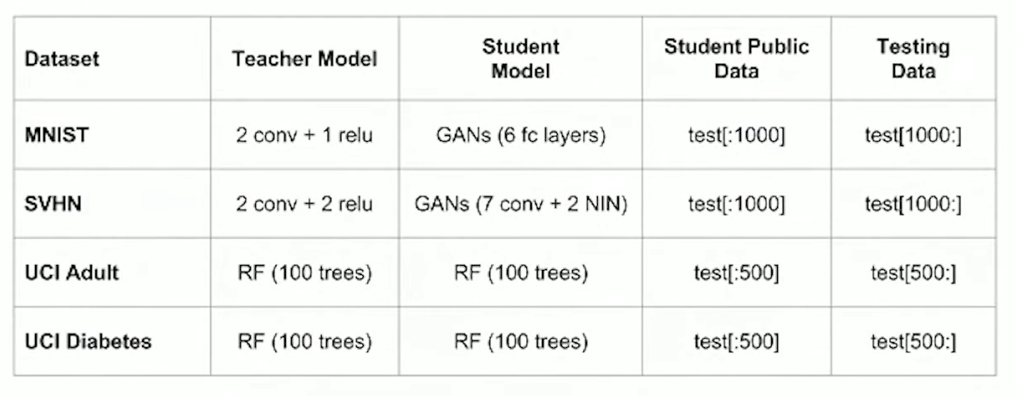
数据集具体设置如下:
- MNIST:10000个测试数据作为公开无标注数据集,学生可以获得其中的9000个数据,在实验中分别随机选取其中100、500或1000个样本的子集使用前面讨论的噪声聚合机制进行标注获得具有伪标签的数据,而它的性能是在测试集剩余1000个样本上评估的。
- SVHN:26,032个测试数据作为公开无标注数据集,学生可以获得其中的10000个数据,在实验中分别随机选取其中500或1000个样本的子集使用前面讨论的噪声聚合机制进行标注获得具有伪标签的数据,而它的性能是在测试集剩余16,032个样本上评估的。
以下的baseline均为通过敏感数据训练获得的结果(即PATE教师集合模型的性能)
Part 1
在对PATE及其变体PATE-G的评估中,首先为每个数据集训练一个教师集合,集合预测的标签的准确性和隐私保障之间的权衡很大程度上取决于集合中教师的数量:训练一批较大数量的教师对于支持注入噪声产生强大的隐私保证,同时对准确性的影响有限是至关重要的;其次通过尽可能少的对教师集合的查询来训练学生,从而最大限度地减少用于学习学生的隐私预算。
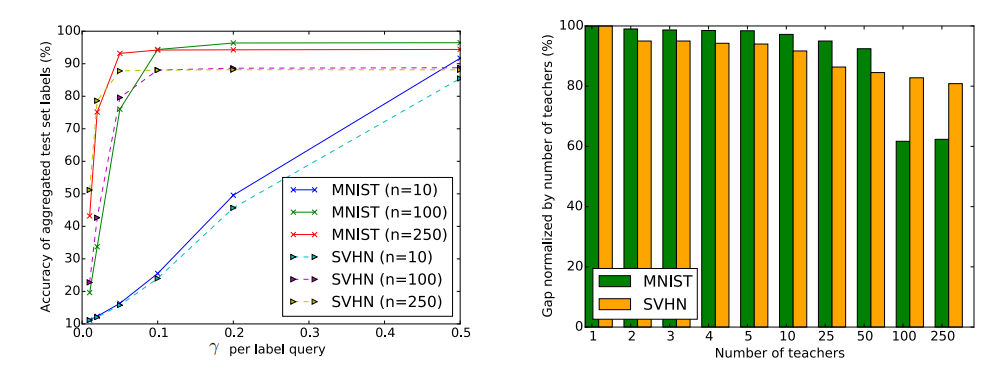
图1. 左:注入噪声的量。在不同的γ值下,折线分别对应MNIST和SVHN两个数据集基于3个不同数量(10/100/250)教师集合噪声聚合的准确性。引入的噪声与γ值成反比:γ值越小对应越大的噪声;右:教师集合的预测的置信度。这个根据获得最多票数的标签和第二多票数的标签之间的数量差距衡量。差距越大,说明教师集合在分配标签时越有信心,对加入的噪声就越鲁棒。可以观察到一个大体的趋势就是教师数量越多,预测的置信度就越高。
part2
噪声聚合机制以保护隐私的方式给学生的无标签训练集贴标签。为了减少花在学生训练上的隐私预算,应对尽可能减少对教师集合的查询。MNIST和SVHN学生的(ε,δ)在差分隐私保证为\((2.04,10^{-5})\)和\((8.19,10^{-6})\)的情况下,达到了98.00%和90.66%的准确率。这些结果提高了这些数据集的差分隐私的最先进水平。Abadi等人(2016)的工作里在MNIST上基于\((8, 10^{-5})\)的差分隐私约束下获得了97%的准确率。Shokri & Shmatikov (2015)报告他们的方法在SVHN上,其每个模型参数满足\(ε>2\)的隐私成本约束,而他们提出的模型有超过30万个参数,达到了约为92%准确率,但粗略的计算这相当于总的隐私成本为\(ε>600,000\)。
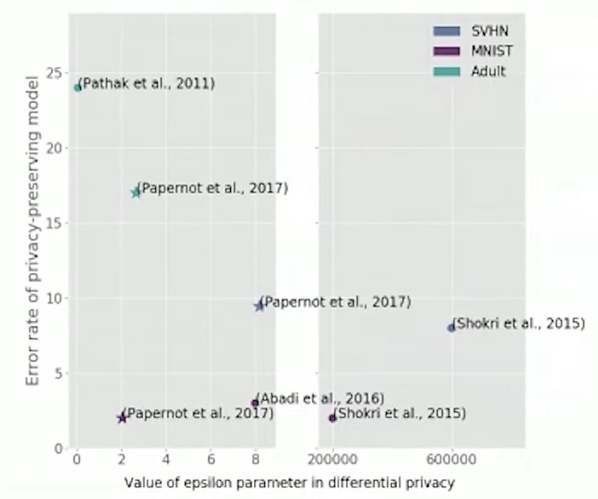
**图2. **相关工作在相同任务下获得的隐私界和错误率。对应如下工作:
-
Abadi et al. (2016)Martin Abadi, Andy Chu, Ian Goodfellow, H. Brendan McMahan, Ilya Mironov, Kunal Talwar, and Li Zhang. Deep learning with differential privacy. In Proceedings of the 2016 ACM SIGSAC Conference on Computer and Communications Security. ACM, 2016.)(DP-SGD)
-
Shokri & Shmatikov (2015)Reza Shokri and Vitaly Shmatikov. Privacy-preserving deep learning. In Proceedings of the 22nd ACM SIGSAC Conference on Computer and Communications Security. ACM, 2015.
-
Pathak et al. (2011)Manas Pathak, Shantanu Rane, Wei Sun, and Bhiksha Raj. Privacy preserving probabilistic inference with hidden markov models. In 2011 IEEE International Conference on Acoustics, Speech and Signal Processing, pp. 5868–5871. IEEE, 2011.
对比之下,PATE方法实现了模型性能和隐私成本的更好的权衡。

表1. 半监督学生的效用和隐私:每一行是用GAN网络以半监督方式训练的学生模型,通过噪声聚集机制向教师进行不同数量的标签查询,最后一列报告了学生的准确性。
Papernot et al., 2018
在这项工作中,基于上面的实验设置引入了一个新的数据集Glyph,这个字符识别任务比以前所有的PATE实验数据集都有一个数量级的类别。Glyph数据集也具有许多现实世界任务所共有的特征:例如,它是不平衡的,一些输入被错误地标记。任务是将输入分类为150个Unicode符号之一。
将经过预处理的数据中6500万个训练数据分配给教师集合,每个教师模型为具有32 leaky ReLU layers的ResNet,将留出的数据分成两个子集,分别为10万和40万个样本:第一个作为公共数据来训练学生,第二个作为其测试数据。
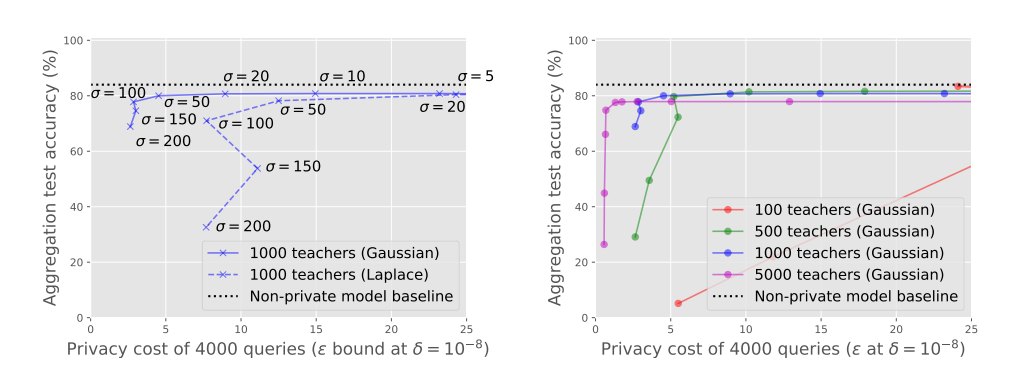
图3:Glyph上LNMax和GNMax聚合器的效用和隐私之间的权衡:噪声分布(左)和教师集合的大小(右)的影响。LNMax聚合器使用拉普拉斯分布,GNMax使用高斯分布。较小的隐私成本ε值(通常通过增加噪声规模σ来获得–见第4节)和较高的精度会更好。
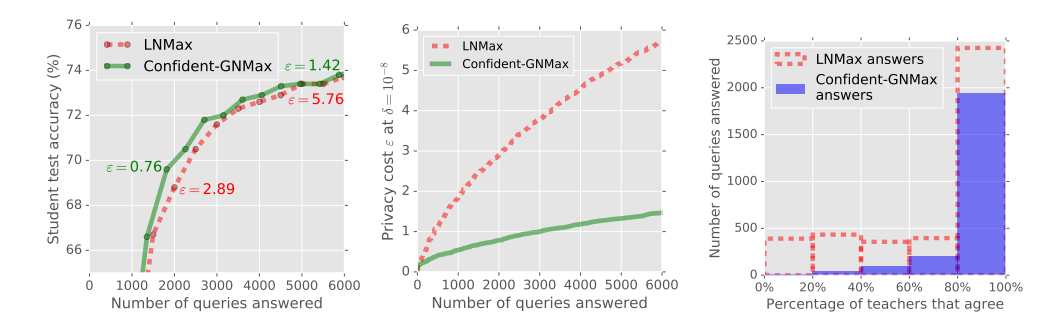
图4:LNMax与Confident-GNMax的对比。左图:在整个训练过程中,隐私得到了极大的改善的同时,准确率也得到了提高(更多内容见表1)。中间:对隐私成本的$ε$差分隐私约束至少是四分之一(更多内容见图5)。右图:直观上的隐私也得到了改善,因为学生在训练时,教师之间的共识要强得多(更多见图5)。这些是字符识别任务的结果,使用最有利的LNMax参数进行公平比较。
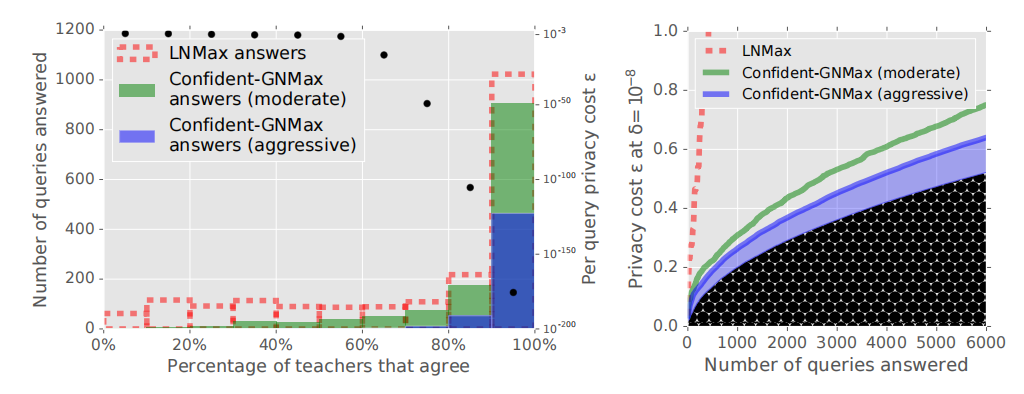
图5:噪声阈值检查的影响。左图:LNMax、Confident-GNMax moderate(T=3500,σ1=1500)和Confident-GNMax aggressive(T=5000,σ1=1500)回答的查询数量。黑点和右轴(按对数比例)显示了在每个bin中回答一个查询的预期成本(通过GNMax,σ2=100)。右图:基于固定数量的回答,回答所有(LNMax)与只回答便宜的查询(GNMax)的隐私成本。曲线下非常暗的区域是选择查询的成本;其余是回答查询的成本。
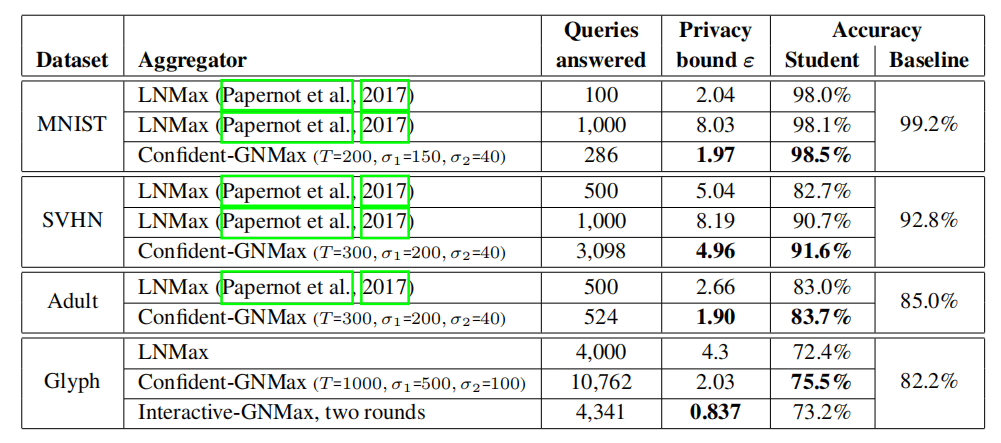
表2. 半监督学生的效用和隐私。注意到其中Glyph学生的准确率仍然比在65M敏感输入上训练的非私有模型的准确率低七个百分点。推测是由于所考虑的数据的未经整理的性质造成的。事实上,类别的不平衡自然需要更多的查询来返回代表度较低的类别的标签。此外,大比例的错误标签输入很可能有很大的隐私成本:这些输入是敏感的,因为它们是分布的异常值,这反映在教师之间对这些输入的弱共识。
代码实现分析
正如上面所介绍的PATE框架由三个关键部分组成。(1) 由n个教师模型组成的集合(2) 聚合机制(3) 学生模型;其中n个教师模型的训练没有什么特别的约束,学生模型的训练也是根据已有的方法进行,可以说聚合机制是整个PATE框架中核心的部分,因此此处的代码分析将集中于PATE的聚合机制及其提供的隐私分析
Papernot et al., 2017
LNMax聚合机制表达式为\(\mathcal{M}_γ(x)\triangleq argmax_i \{n_i(x) + \operatorname{Lap}\left(\frac{1}{\gamma}\right)\}\)
这种聚合机制采用对相同输入进行推理所产生的几个模型的softmax/logit输出,每个模型为样本选择一个标签,所有模型一起进行投票操作,然后将拉普拉斯噪声加入标签计数,并返回最多投票的标签。
def noisy_max(logits, lap_scale, return_clean_votes=False):
"""
:param logits: 每个样本的对数或概率
:param lap_scale: 将添加到计数中的拉普拉斯噪声的尺度
:param return_clean_votes: 如果设置为 "True"会返回干净的投票(无Laplacian noise)。利用这 个值可以进行这个聚合机制的隐私分析。
:return: result, 加入随机laplace噪声后的投票结果
clean_votes, 不包含噪声的投票结果
labels:教师集合生成的原始标签
"""
# Compute labels from logits/probs and reshape array properly
labels = labels_from_probs(logits)
labels_shape = np.shape(labels)
labels = labels.reshape((labels_shape[0], labels_shape[1]))
# Initialize array to hold final labels
result = np.zeros(int(labels_shape[1]))
if return_clean_votes:
# Initialize array to hold clean votes for each sample
clean_votes = np.zeros((int(labels_shape[1]), 10))
# Parse each sample
for i in xrange(int(labels_shape[1])):
# Count number of votes assigned to each class
label_counts = np.bincount(labels[:, i], minlength=10)
if return_clean_votes:
# Store vote counts for export
clean_votes[i] = label_counts
# Cast in float32 to prepare before addition of Laplacian noise
label_counts = np.asarray(label_counts, dtype=np.float32)
# Sample independent Laplacian noise for each class
for item in xrange(10):
label_counts[item] += np.random.laplace(loc=0.0, scale=float(lap_scale))
# Result is the most frequent label
result[i] = np.argmax(label_counts)
# Cast labels to np.int32 for compatibility with deep_cnn.py feed dictionaries
result = np.asarray(result, dtype=np.int32)
if return_clean_votes:
# Returns several array, which are later saved:
# result: labels obtained from the noisy aggregation
# clean_votes: the number of teacher votes assigned to each sample and class
# labels: the labels assigned by teachers (before the noisy aggregation)
return result, clean_votes, labels
else:
# Only return labels resulting from noisy aggregation
return result
基于clean_votes的值就可以进行隐私分析,接下来介绍对应3.2小结中利用moments accountant对于隐私成本的统计和分析的代码实现
logmgf_from_counts这个函数就是基于教师集合的投票结果,以及拉普拉斯噪声尺度来计算对应的moment accountant的值。
def logmgf_from_counts(counts, noise_eps, l):
"""
:param counts: 教师集合不包含噪声的投票结果
:param noise_eps: 将添加到计数中的拉普拉斯噪声的尺度
:param l: moments accountant的次数
:return:
"""
q = compute_q_noisy_max(counts, noise_eps)
return logmgf_exact(q, 2.0 * noise_eps, l)
其中compute_q_noisy_max这个函数就是计算上式对应的q的值,q为\(\operatorname{Pr}\left[\mathcal{M}(d) \neq j^{*}\right]\),q的计算对应于定理3,即计算下面这个式子的右边的部分。
def compute_q_noisy_max(counts, noise_eps):
"""returns ~ Pr[outcome != winner].
Args:
counts: a list of scores
noise_eps: privacy parameter for noisy_max
Returns:
q: the probability that outcome is different from true winner.
"""
# For noisy max, we only get an upper bound.
# Pr[ j beats i*] \leq (2+gap(j,i*))/ 4 exp(gap(j,i*)
# proof at http://mathoverflow.net/questions/66763/
# tight-bounds-on-probability-of-sum-of-laplace-random-variables
winner = np.argmax(counts)
counts_normalized = noise_eps * (counts - counts[winner])
counts_rest = np.array(
[counts_normalized[i] for i in xrange(len(counts)) if i != winner])
q = 0.0
for c in counts_rest:
gap = -c
q += (gap + 2.0) / (4.0 * math.exp(gap))
return min(q, 1.0 - (1.0 / len(counts)))
logmgf_exact函数计算最终的矩会计的整体上界约束,计算这个约束取了三个项的最小值:
- 基于定理1中\(\alpha(l;aux,d,d')\le2\gamma^2l(l+1)\)的式子的右边计算出来的界
- 基于经过上面函数计算返回的q值,基于节中定理2中\(\alpha\left(l ; a u x, d, d^{\prime}\right) \leq \log \left((1-q)\left(\frac{1-q}{1-e^{2 \gamma} q}\right)^{l}+q \exp (2 \gamma l)\right)\)式子的右边计算出来的界
- 基于基本的差分隐私保证获得的界,即在\(l\)阶下的矩会计值为\(\varepsilon*l\)
def logmgf_exact(q, priv_eps, l):
"""Computes the logmgf value given q and privacy eps.
Args:
q: pr of non-optimal outcome
priv_eps: eps parameter for DP
l: moment to compute.
Returns:
Upper bound on logmgf
"""
if q < 0.5:
t_one = (1 - q) * math.pow((1 - q) / (1 - math.exp(priv_eps) * q), l)
t_two = q * math.exp(priv_eps * l)
t = t_one + t_two
try:
log_t = math.log(t)
except ValueError:
print("Got ValueError in math.log for values :" + str((q, priv_eps, l, t)))
log_t = priv_eps * l
else:
log_t = priv_eps * l
return min(0.5 * priv_eps * priv_eps * l * (l + 1), log_t, priv_eps * l)
正如3.1小结中介绍了Papernot et al., 2017中利用矩会计的隐私分析流程框架,我们经过上面几个函数的计算相当于获得了对应阶\(\lambda\)下的矩会计的值,这里对于一个查询的矩会计计算的阶数设置为了整数1-8,也就是需要分别在这8个\(\lambda\)值下计算对应的矩会计结果,然后就是根据定理1中矩会计的组成性,累计对应阶下的矩会计值。最后就需要结合矩会计中的尾界,即式子\(\delta=\min _{\lambda} \exp \left(\alpha_{\mathcal{M}}(\lambda)-\lambda \varepsilon\right)\),推导出最优的\((\varepsilon,\delta)\)-差分隐私保证。
这里一般是给定\(\delta\)的值然后根据一系列\(\lambda\)值下的矩会计总计的结果推导出最优的隐私成本,也就是\(\varepsilon\)值,以下展示总体计算过程的简化版本。
def main(unused_argv):
# Binaries for MNIST results
paper_binaries_mnist = []
if FLAGS.counts_file == "mnist_250_teachers_labels.npy" \
or FLAGS.indices_file == "mnist_250_teachers_100_indices_used_by_student.npy":
maybe_download(paper_binaries_mnist, os.getcwd())
#示例代码中将教师集合投票的结果存成了本地的文件,
#下面进行的是一些文件读取和初始化工作
counts_mat = np.load(FLAGS.counts_file)
n = counts_mat.shape[0]
num_examples = min(n, FLAGS.max_examples)
indices = np.array(range(num_examples))
l_list = 1.0 + np.array(xrange(FLAGS.moments))#矩估计的阶,这里取1-8
beta = FLAGS.beta
total_log_mgf_nm = np.array([0.0 for _ in l_list])
total_ss_nm = np.array([0.0 for _ in l_list])
noise_eps = FLAGS.noise_eps
#indices对应聚合机制预测的样本的编号
for i in indices:
total_log_mgf_nm += np.array(
[logmgf_from_counts(counts_mat[i], noise_eps, l)
for l in l_list])
delta = FLAGS.delta
"""
(Pdb) total_log_mgf_nm 分别对应阶数为1-8下的矩估计值
array([0.23448107, 0.63579189, 1.20133063, 1.83118012, 2.53420024,
3.26710464, 4.03590102, 4.8755633 ])
"""
# We want delta = exp(alpha - eps l).
# Solving gives eps = (alpha - ln (delta))/l
eps_list_nm = (total_log_mgf_nm - math.log(delta)) / l_list
"""
(Pdb) eps_list_nm 基于矩估计值和差分隐私中的delta计算获得对应的差分隐私界
array([11.74740653, 6.07435868, 4.23808537, 3.3360264 , 2.80942514,
2.46333835, 2.22126093, 2.0485611 ])
"""
print("Epsilons (Noisy Max): " + str(eps_list_nm))
#取eps_list_nm中最小的值则为最优的差分隐私界
print("Epsilon = " + str(min(eps_list_nm)) + ".")#Epsilon = 2.048561096236246.
if min(eps_list_nm) == eps_list_nm[-1]:
print("Warning: May not have used enough values of l")
# 以下计算的是无数据依赖的差分隐私界,可以观察到这里的隐私界比上面的隐私界大了非常多
# 2*noise_eps DP.
data_ind_log_mgf = np.array([0.0 for _ in l_list])
data_ind_log_mgf += num_examples * np.array(
[logmgf_exact(1.0, 2.0 * noise_eps, l) for l in l_list])
data_ind_eps_list = (data_ind_log_mgf - math.log(delta)) / l_list
print("Data independent bound = " + str(min(data_ind_eps_list)) + ".")
#Data independent bound = 51.51292546497024.
return
Papernot et al., 2018
TODO
总结
本文介绍了教师集合隐私聚合(Private Aggregation of Teacher Ensembles,PATE)这个能够在分类任务保护其训练数据的一种学习框架,PATE的优点是能够从独立的 “教师 “模型的聚合共识中学习,这些教师模型在无交集的数据上训练,既能提供直观的隐私保证,又与底层机器学习技术无关。同时利用半监督学习技术,将教师集合的知识迁移到学生模型,这样子既固定了隐私的成本,保护了基于敏感数据训练的教师集合的隐私,又能够实现较好的模型性能。
其中对于PATE的隐私分析是非常保守的,因其假设了一个能够进行不限次数查询并且能够访问模型内部参数的强大的攻击对手,还悲观的假设了,即使一个教师的训练集中有一个样本发生变化,该教师产生的分类结果也可能改变。这个方法的一个优势在于,隐私分析无需对于教师的进行任何假设,这使得它具有广泛的适用性,进一步在具体情况下,作者提出或许可以做出更强的隐私保证,比如对教师所用的学习算法做出假设的时候。
附录
sensitivity
差分隐私保护可以通过在查询函数的返回值中加入适量的干扰噪声来实现。加入噪声过多会影响 结果的可用性,过少则无法提供足够的安全保障。敏感度是决定加入噪声量大小的关键参数,它指删除 数据集中任一记录对查询结果造成的最大改变。在差分隐私保护方法中定义了两种敏感度,即全局 敏感度(Global Sensitivity)和局部敏感度(local Sensitivity)。
(定义)全局敏感度。设有函数$f:D\to R^d$,输入为一数据集,输出为一$d$维向量。对于任意的邻近数据集$D$和$D’$
\[G S_{f}=\max _{D, D^{\prime}}\left\|f(D)-f\left(D^{\prime}\right)\right\|_{1}\]称为函数$f$的全局敏感度,其中$\left|f(D)-f\left(D^{\prime}\right)\right|_{1}$是$f(D)$和$f(D’)$之间的1阶范数距离。
函数的全局敏感度由函数本身决定,不同的函数会有不同的全局敏感度,一些函数具有较小的全局敏感度(例如计数函数,全局敏感度为1),因此只需要添加少量的噪声就可以掩盖因一个记录被删除对查询结果产生的影响,实现差分隐私保护。但对某些函数而言,例如求平均值、求中位数等函数,则往往具有较大的全局敏感度。当全局敏感度较大时,必须在函数输出中添加足够大的噪声才能保证隐私安全,导致数据可用性较差,针对这个问题,Nissim等人定义了局部敏感度以及其对计算相关的其他概念。
(定义)局部敏感度。设有函数$f:D\to R^d$,输入为一数据集,输出为一$d$维向量。对于任意的邻近数据集$D$和$D’$
\[L S_{f}=\max _{ D^{\prime}}\left\|f(D)-f\left(D^{\prime}\right)\right\|_{1}\]称为函数$f$在$D$上的局部敏感度,局部敏感度由函数$f$和给定数据集$D$中具体数据共同决定,由于利用了数据集的数据分布特征,局部敏感度通常要比全局敏感度小得多。局部敏感度和全局敏感度的关系可以表示为
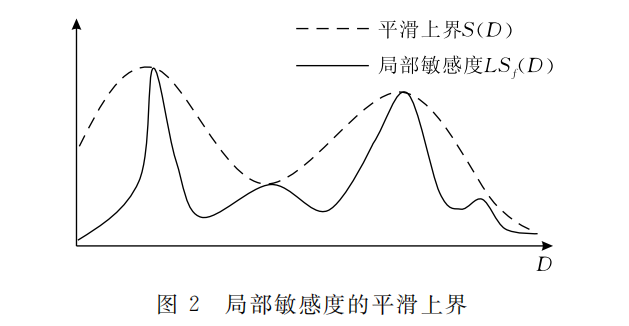
\[G S_{f}=\max _{D}(L S_{f}(D))\]但是,由于局部敏感度在一定程度上体现了数据分布的特征,如果直接应用局部敏感度来计算噪声会泄露数据集中的敏感信息,因此局部敏感度的平滑上界(Smooth Upper Bound)被用来与局部敏感度一起确定噪声量的大小。
(定义)平滑上界。给定数据集$D$及其任意邻近数据集$D’$,函数$f$的局部敏感度为$L S_{f}(D)$,对于$\beta>0$,若函数$S:D\to R$满足$S(D)\ge LS_f(D)$且$S(D)\le e^{\beta}S(D’)$,则称$S$为函数$f$的局部敏感度的$\beta$-平滑上界
所有满足这一定义的函数都可以被定义为平滑上界,将局部敏感度代入次函数中则可以得到平滑敏感度(Smooth sensitivity),进而用于计算噪声大小。平滑上界和局部敏感度的关系如下图所示。Nissim 在文中给出了一个平滑上界的例子,并以此生成了平滑敏感度。
(定义)平滑敏感度。给定数据集\(D\)即\(D'\),函数称为函数\(f\)的\(\beta\)平滑敏感度,其中\(\beta>0\)