Adversarial robustness survey：对抗样本、对抗训练和对抗鲁棒性介绍

Posted on | In |

随着深度学习技术的不断深入发展，神经网络在越来越多的领域中发挥着重要的作用，如计算机视觉、自然语言处理等，尤其是在很多与安全相关的环境中有着实际应用，如手机支付、自动驾驶汽车、无人机侦察等，同时深度神经网络的安全逐渐成为人工智能安全问题中研究的重点。

然而，随着对人工智能研究的不断深入，人们发现人工智能技术仿佛一把达摩克里斯之剑，在带来便利 的同时也带来了安全隐患，如数据投毒(data poisoning)、模型窃取(model theft)、后门攻击(backdoor attacks)、对抗样本(adversarial examples)等。在这些攻击中，尤其以对抗样本攻击最为著名。

对抗样本指在原有数据对象上添加人眼无法察觉的细微扰动而产生的新数据对象，人工智能模型对这些 细微扰动十分敏感，因此导致了错误预测结果。通过构造对抗样本对深度神经网络进行攻击的方法，一 般称为对抗攻击(adversarial attack)。

screenshot

对抗样本的存在揭示了深度神经网络模型的脆弱性，给其在安全敏感领域的广泛部署带来巨大安全隐 患。比如 图像对抗样本的存在不仅极大地影响了图像识别分类 应用效果，而且还严重威胁到了人们的人 身和财产安全。例 如，在自动驾驶场景中，攻击者将路标改造成相应的对抗样本，造成自动驾驶系统对 路标产生错误判断，从而导致交通事故发生。

screenshot

本次报告将进行围绕着抗鲁棒性（Adversarial Robustness）相关内容的介绍

  • 问题定义
  • 构造对抗样本的方法
  • 基于对抗样本进行对抗训练
  • 关于对抗鲁棒模型进一步研究

本文由本人完成，欢迎随意转载阅读^ - ^

1. 问题定义

1.1 机器学习风险

机器学习风险：

\[R(h_\theta) = \mathbf{E}_{(x,y)\sim\mathcal{D}}[\ell(h_\theta(x)),y)]\]

其中$\mathcal{D}$表示样本的真实分布。在实际中，我们无法获知样本的真实分布，因此我们从真实 分布中采样一部分样本构造一个有限的集合来近似描述$\mathcal{D}$：

\[D = \{(x_i,y_i) \sim \mathcal{D}\}, i=1,\ldots,m\]

经验风险(empirical risk)：

在有限集合$D$上计算得到的损失就是所谓的经验损失。一般会将有限集合$D$划分成训练集 $D_{\mathrm{train}}$和测试集$D_{\mathrm{test}}$，机器学习算法就是在寻找能够最小化训练集上 经验误差$D_{\mathrm{train}}$的参数：

\[\hat{R}(h_\theta,D) = \frac{1}{|D|}\sum_{(x,y) \in D} \ell(h_\theta(x)),y).\\ \text{minimize}_\theta \hat{R}(h_\theta, D_{\mathrm{train}}).\]

模型训练结束后，通过测试集$D_{\mathrm{test}}$来估计风险$R(h_{\theta})$。

1.2对抗风险

对抗风险的定义：

\[R_{\mathrm{adv}}(h_\theta) = \mathbf{E}_{(x,y)\sim\mathcal{D}}\left[\max_{\delta \in \Delta(x)} \ell(h_\theta(x + \delta)),y) \right ]\]

这里不再只考虑每个样本点上的损失$\ell(h_\theta(x), y)$，而是考虑在样本点周围一定范围内的最差情 况的损失，因为对抗样本的就是要对模型进行攻击，因此这里就需要去最大化损失。

对抗经验风险的定义：

\[\hat{R}_{\mathrm{adv}}(h_\theta, D) = \frac{1}{|D|}\sum_{(x,y)\in D} \max_{\delta \in \Delta(x)} \ell(h_\theta(x + \delta)),y) .\]

上式可以理解为，在模型参数固定的情况下，在允许的扰动范围$\Delta(x)$内对每个输入样本进行对抗 扰动，分类器取每个输入的最差情况（也就是导致损失最大的那个对抗样本）来计算经验损失。

1.3 对抗训练

对抗训练目标是使得模型具有对抗鲁棒性，从而能够抵抗对抗样本的攻击。和传统训练类似，可以将表 示成如下的优化问题：

\[\text{minimize}_\theta \hat{R}_{\mathrm{adv}}(h_\theta, D_{\mathrm{train}}) \equiv \text{minimize}_\theta \frac{1}{|D_{\mathrm{train}}|}\sum_{(x,y)\in D_{\mathrm{train}}} \max_{\delta \in \Delta(x)} \ell(h_\theta(x + \delta)),y) .\]

将其称为对抗学习的最小-最大(min-max)优化公式，或鲁棒优化公式。

和传统训练一样，可以通过随机梯度下降来求解该优化问题：

\[\theta := \theta - \frac{\alpha}{|B|} \sum_{(x,y)\in B} \nabla_\theta \max_{\delta \in \Delta(x)} \ell(h_\theta(x + \delta)),y).\]

其中$B \subseteq D_{\mathrm{train}}$是一个minibatch。

但如何在内部项是一个最大化问题的情况下求取其梯度?

根据Danskin’s theorem，上述内部项的梯度就是内部项在最大值时的梯度。换句话说，令 $\delta^*$表示这个内部最大优化问题的最优解：

\[\DeclareMathOperator*{\argmax}{argmax} \delta^\star = \argmax_{\delta \in \Delta(x)} \ell(h_\theta(x + \delta)),y)\]

于是，模型参数的梯度就对应于：

\[\nabla_\theta \max_{\delta \in \Delta(x)} \ell(h_\theta(x + \delta)),y) = \nabla_\theta \ell(h_\theta(x + \delta^\star)),y)\]

这里有一个很微妙的点，就是我们在计算梯度时不需要考虑$\delta^$对$\theta$的依赖，但事实上计 算$\delta^$的确是依赖$\theta$的。具体可以参考Danskin’s theorem的具体证明，这里只需要知道 Danskin’s theorem让求解这个问题变得更容易了。

于是，整个训练框架如下所示

  1. 对每个$x,y \in B$，求解内部的最大化问题(即计算对抗样本)

    \[\delta^\star(s) = \argmax_{\delta \in \Delta(x)} \ell(h_\theta(x + \delta)),y)\]

  2. 计算经验对抗风险的梯度，并更新$\theta$

    \[\theta := \theta - \frac{\alpha}{|B|} \sum_{(x,y)\in B} \nabla_\theta \ell(h_\theta(x + \delta^\star(x))),y).\]

具体训练过程就是反复地重复以上两个步骤。这里需要注意的几点：

  • 首先，事实上我们并没有对真正的经验对抗风险做梯度下降，因为我们通常无法最优求解内部的最 大化问题
  • 在一定范围内求解网络的损失最大值一个非凸优化问题，一般通过梯度下降求解，最多只能找到局 部最优点；又因为Danskin’s theorem只在有内部最大化问题被最优求解的前提下才能使用，这似 乎带来了问题
  • 在实际中，对抗训练的效果依赖于内部最大化问题在何种程度上被”较好”地求解。如果内部优化问 题求解得不好，那么攻击者可以用更好的策略对内部问题进行求解就会实现有效的攻击

2. 构造对抗样本：一个约束优化问题

2.1 求解内部最大化问题

当假设函数$h_\theta$是神经网络时，该如何（近似地）求解内部优化问题？

有三种主要的策略来解决，分别对应着下界，精确解和上界

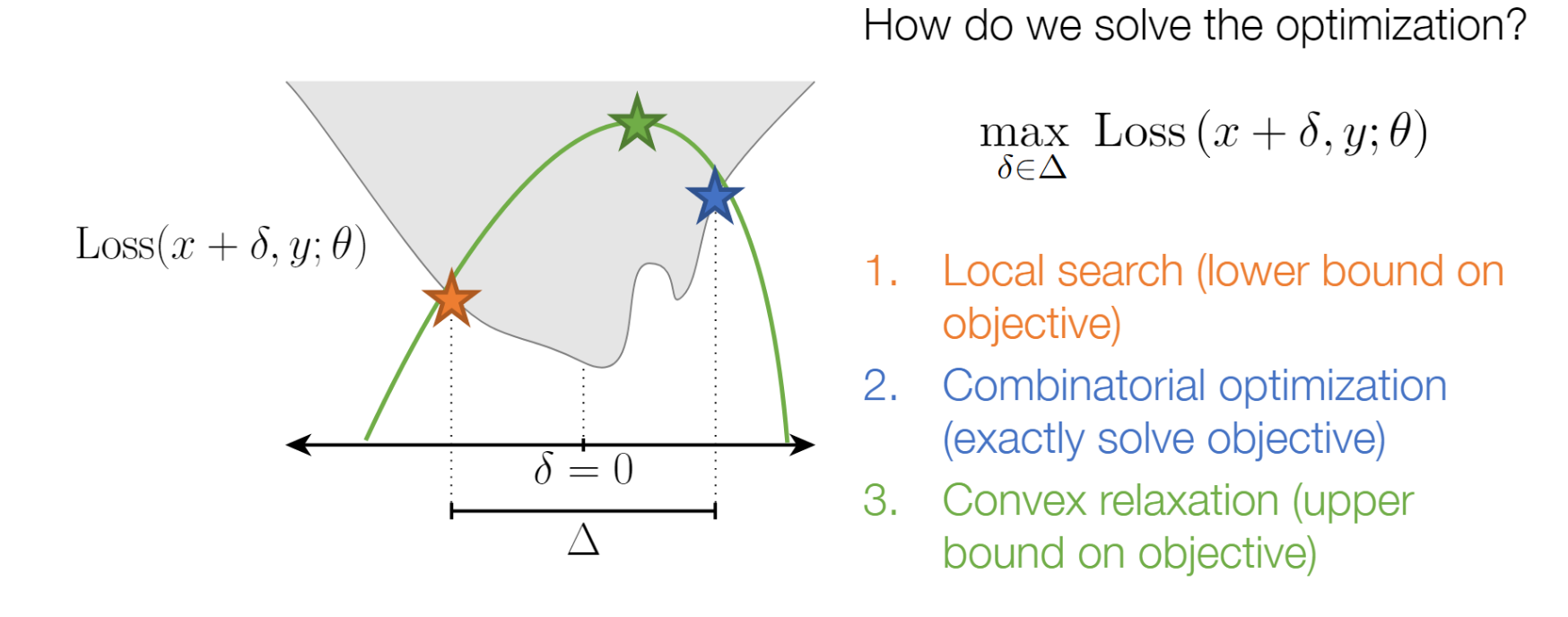
截屏2023-01-29 15.55.09

  • *找到内部最大化的下界*,对应于求解对抗样本，这也许是求解$\DeclareMathOperator*{\maximize} {maximize} \maximize_{|\delta| \leq \epsilon} \ell(h_\theta(x + \delta), y)$最简单直接的方法了。 任何可行的$\delta$都会给出一个下界，所以我们可以“经验地来求解优化问题”，即“找到某个对抗样 本”，这也是目前最常用的求解内部最大化问题的策略。
  • ***精确地求解这个优化问题***，这种方法非常具有挑战性，但其实对于具有许多激活函数的网络损失函数而 言，我们都可以将最大化问题形式化为一个组合优化问题，并通过混合整数规划（mixed integer programming）这样的技巧来精确求解。虽然这类方法在扩展到大型模型时会面临巨大挑战，但是对于 小的问题，它们强调了一个重要的观点，即在某些情况下可以构造出内部最大化问题的精确解。
  • *找到优化目标的上界*，这个基本策略是考虑一个松弛的网络结构，使得这个松弛版本的网络既包含原本 的网络，同时其构建方式也使得这个问题在这种情况下更易于精确地优化。不同的是，这类方法通常不 会给出真实网络的对抗样本（因为它们所操作的是松弛的模型，不同于原始模型）。

2.2 构造对抗样本（找到内部最大化的下界）

快速梯度符号法（Fast Gradient Sign Method）

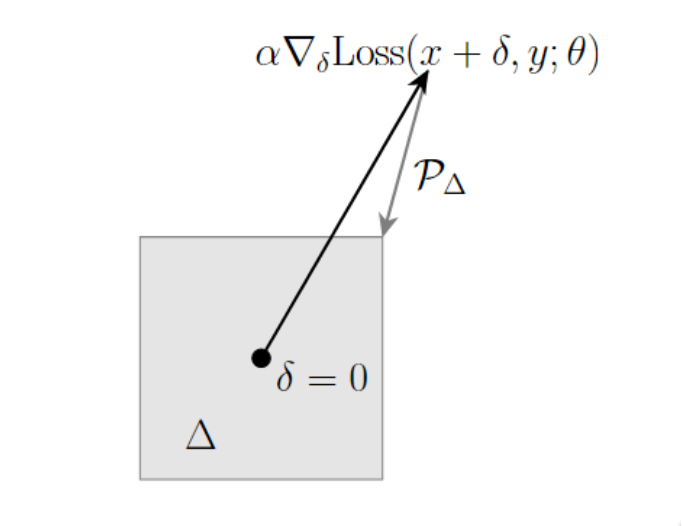
screenshot

快速梯度符号法(Fast Gradient Sign Method，FGSM)，它是深度学习领域中最早提出的构造对抗样 本的方法之一，由Goodfellow等在ICLR 2015会议上提出。FGSM方法沿着梯度反方向添加扰动使损失 函数快速增大，最终导致模型分类错误。

具体来说就是，首先固定网络参数，计算出损失关于扰动$\delta$的梯度：

\[g := \nabla_\delta \ell(h_\theta(x + \delta),y)\]

为了最大化损失，需要让$\delta$在梯度的方向上以一定的步长$\alpha$迈出一步（take a step）：

\[\delta := \delta + \alpha g\]

当然还需要保证更新后的$\delta$在一定的约束范围内$|\delta| \leq \epsilon$，这里用到的约束就是 扰动的无穷范数$\ell_\infty$

\[\delta := \mathrm{clip}(\alpha g, [-\epsilon, \epsilon]).\]

现在的问题是，步长应该取多大？如果我们想要让损失尽可能大的话，就应该取尽可能大的$\alpha$。 如果取了一个很大的$\alpha$，由于约束，就会被重新裁剪回$[-\epsilon, \epsilon]$内，这时候$g$对 于更新的影响就只剩下决定符号正负了（也就是说$g$的大小相较于$\alpha$变得不再重要）。

于是，当取一个很大的$\alpha$时，更新就可以表示为：

\[\delta := \epsilon \cdot \mathrm{sign}(g).\]

虽然此攻击方法可以快速生成对抗样本，但由于是单步攻击，计算所得扰动并不精准，导致攻击成功率 较低。

关于FGSM的几点说明：

第一，FGSM是针对无穷范数$\ell_\infty$下的攻击所设计的，因为FGSM只是在$\ell_\infty$约束下的一 步更新。不过也可以将其推广到其它范数情况下，后续会进一步说明。

第二，FGSM基于的假设是，在$x$点处计算的梯度方向上的线性近似是损失函数在整个约束区域 $|\delta|_\infty \leq \epsilon$内的一个合理的近似，但对于神经网络而言，事实并不如此，因为即使 在一块很小的区域内损失平面也不是线性的。换句话说就是，在$x$这一点上的确算出了梯度下降的方 向，但朝着这个方向走一步后，这个方向很大可能已经不再是最优的方向了。如果想要得到更好的对抗 样本，这种仅做一步更新并裁剪的方法还远远不够。

投影梯度下降（Projected gradient descent）

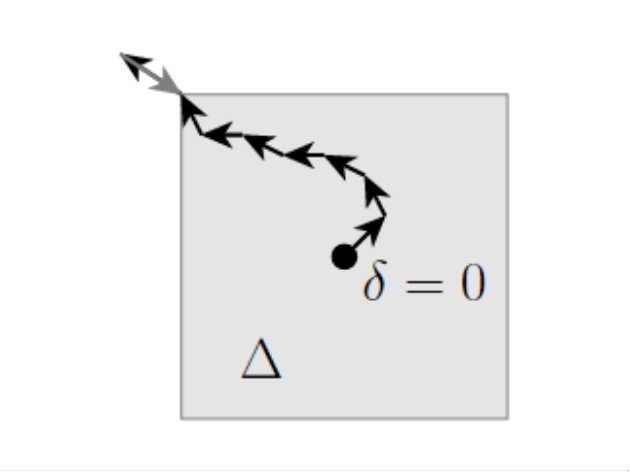
screenshot

上述讨论引出了投影梯度下降（PGD）这个构造对抗样本方法。和上述过程类似，这个方法只是从一步 变成了迭代、从大步长变成了小步长。基本的PGD算法就是重复如下过程：

\[% <![CDATA[ \begin{split} & \mbox{Repeat:} \\ & \quad \delta := \mathcal{P}(\delta + \alpha \nabla_\delta \ell(h_\theta(x+\delta), y)) \end{split} %]]>\]

其中$\mathcal{P}$表示约束至范围内的投影操作project（例如针对无穷范数$\ell_\infty$的裁剪 clip）。在PGD中可以指定诸如步长、迭代次数等参数。可以看一下PGD具体的实现：

def pgd(model, X, y, epsilon, alpha, num_iter):    
		""" Construct FGSM adversarial examples on the examples X"""    
		delta = torch.zeros_like(X, requires_grad=True)    
    for t in range(num_iter):        
        loss = nn.CrossEntropyLoss()(model(X + delta), y)        
        loss.backward()        
        delta.data = 
        (delta +X.shape[0]*alpha*delta.grad.data).clamp(epsilon,epsilon)        
        delta.grad.zero_()    
    return delta.detach()

但是我们一般不直接采用上面通过在梯度方向上反复迭代的这种PGD实现

\[z := z - \alpha \nabla_z f(z).\]

因为这里对梯度值的尺度很敏感，并且这个梯度在原始数据点上通常很小，需要根据梯度值的尺度来调整步长。因此这里引入了最速下降（steepest descent），基于这个方法，可以将$\ell_2$范数约束下 的扰动更新表示为：

\[\DeclareMathOperator*{\argmax}{argmax} z := z - \argmax_{\|v\| \leq \alpha} v^T \nabla_z f(z).\]

如果使用$\ell_\infty$来约束，那么该更新为:

\[\argmax_{\|v\|_2 \leq \alpha} v^T \nabla_z f(z) = \alpha \frac{\nabla_z f(z)}{\|\nabla_z f(z)\|_2}\] 
def pgd(model, X, y, epsilon, alpha, num_iter):    
		""" Construct FGSM adversarial examples on the examples X"""    
		delta = torch.zeros_like(X, requires_grad=True)    
    for t in range(num_iter):        
        loss = nn.CrossEntropyLoss()(model(X + delta), y)        
        loss.backward()        
        delta.data = 
        (delta + alpha*delta.grad.detach().sign()).clamp(-epsilon,epsilon)        
        delta.grad.zero_()    
    return delta.detach()

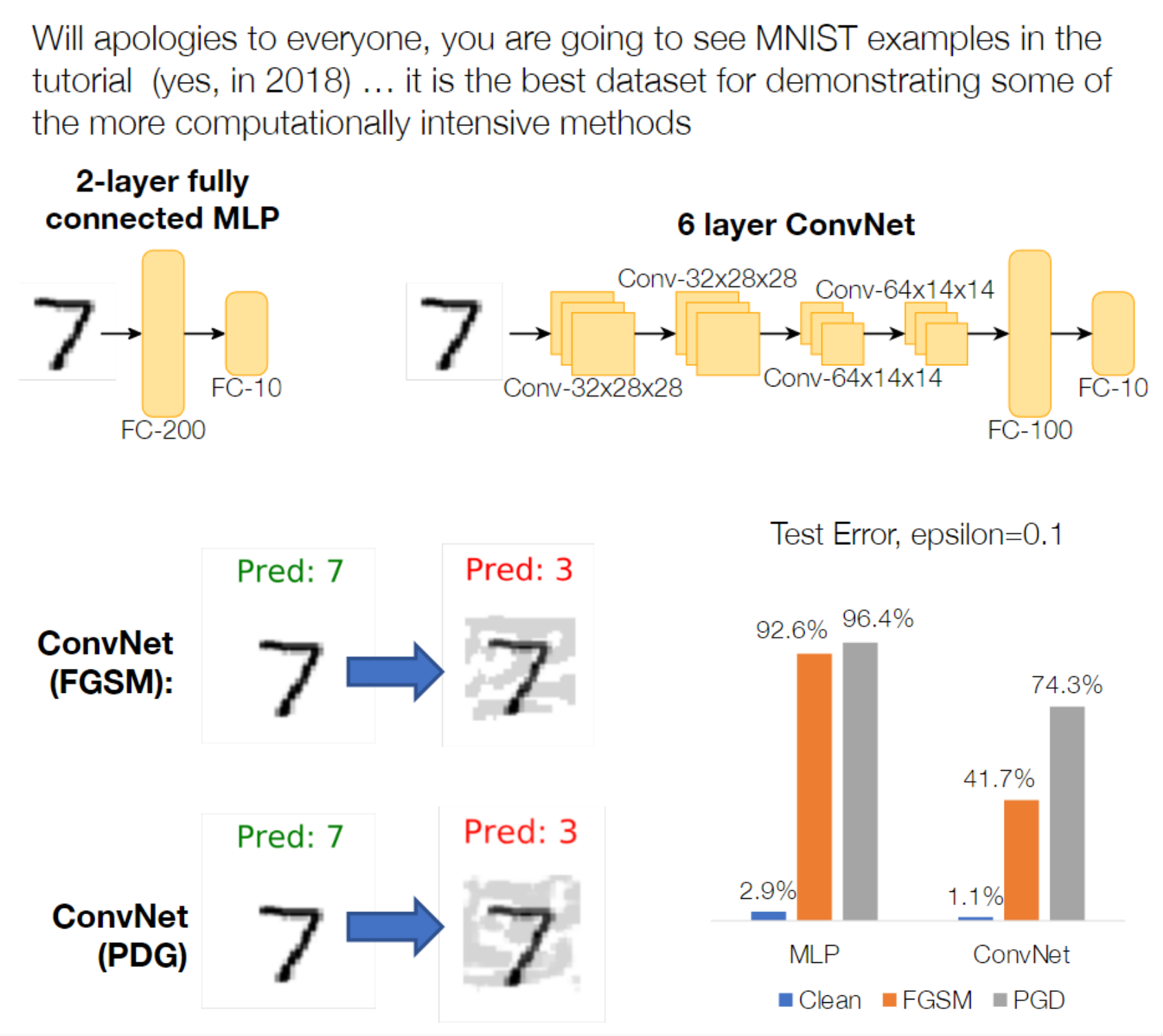
screenshot

研究表明，PGD是非常强的first-order攻击，能防御PGD攻击的网络，就可以防御其他任何first-order攻击，所以在防御时很多工作都会用PGD进行对抗训练。

针对性攻击（Targeted Attack）

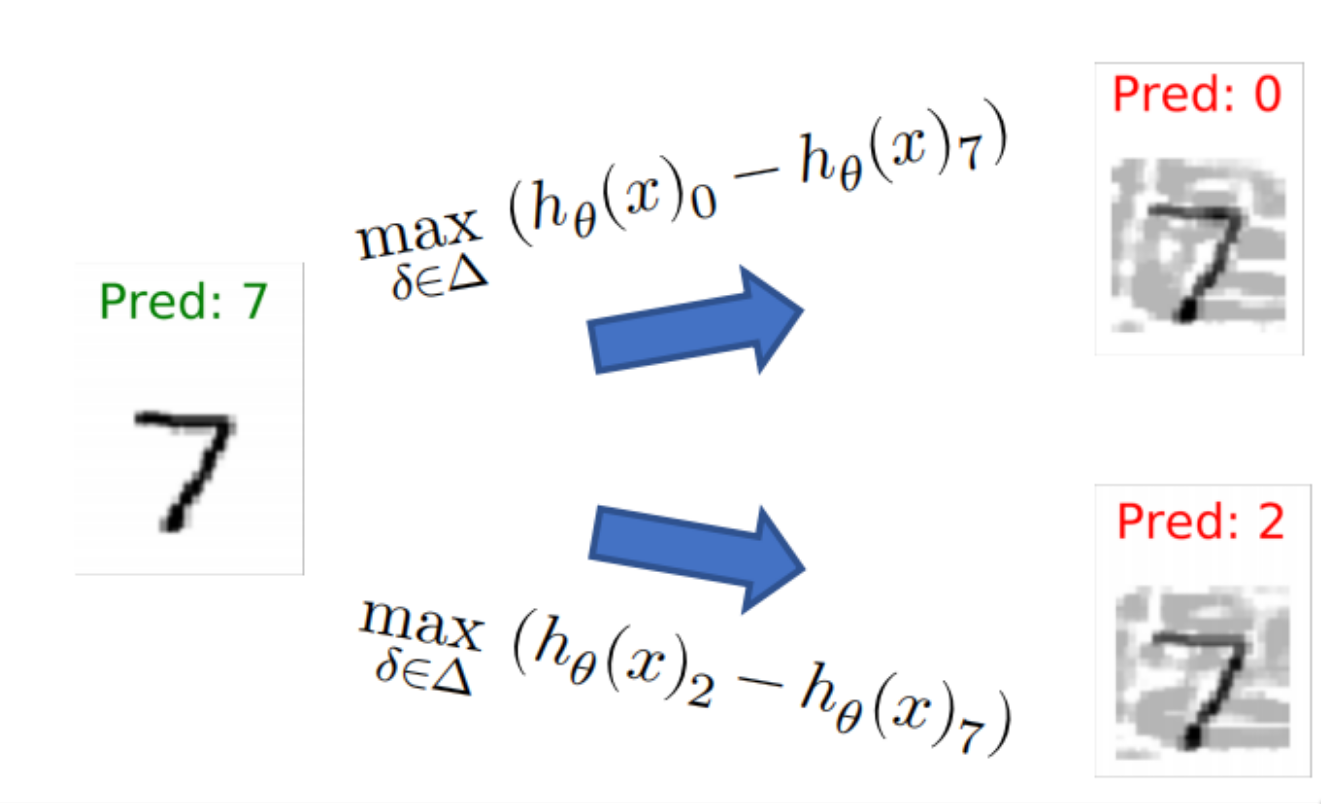
上面的两种都是非针对性攻击（Non-targeted attack），也就是只要把让模型把标签预测错误即可。这 里我们可以通过修改一下损失函数让模型错误预测为指定的类别：

screenshot

Non-$ℓ_∞$ norms

截至目前，我们大部分都在考虑对$\delta$的无穷范数$\ell_\infty$进行约束，而这里我们可以将 $\ell_\infty$换成任意的范数约束，从而实现不一样的约束效果，比如说$\ell_2$和$\ell_0$范数约束

$\ell_2$范数：向量各元素的平方和然后求平方根，$\Delta = {\delta : |\delta|_2 \leq \epsilon}$ 限制原始样本和扰动后的样本的欧氏距离

$\ell_0$范数：向量中非0的元素的个数–》$\Delta = {\delta : |\delta|_0 \leq \epsilon}$限制 改变的样本点数量

$\ell_\infty$范数：向量中各个元素绝对值的最大值–》$\Delta = {\delta : |\delta|_\infty \leq \epsilon}$限制扰动向量中各个元素变化的最大量

screenshot

这个例子中的一个关键点是，$\ell_\infty$攻击导致的扰动几乎分布在整个图像上；而$\ell_2$攻击造成 的扰动发生在图像的局部，因为$\ell_2$可以平衡某些点处大的扰动和另一些点处小的扰动。这是不同约 束带来的不同扰动特性。

关于扰动的选取其实是对抗样本中一个最本质的问题

早期的研究为了去更方便地且直观地认识对抗样本现象，不管是从理论上还是从实验上，都习惯于选择 使用 $\ell_p$ 范数作为约束。但是 $\ell_p$ 范数并不适合许多结构性很强的高维数据，比如图像。 而且在 $\ell_p$ 范数下对所有样本使用同一个 $\epsilon$ 也是不合理的，有些样本天然离分类面近， 一个很小的扰动就改变它的label了；而有些样本天然离分类面远，可以忍受较大的扰动；少量文章对这 件事做了初步探索。 如何去构造和人类感知相近的对抗样本还有很大的探索空间。

其他构造对抗样本方法

事实上这个研究领域发展到现在，提出了各种各样的对抗样本的构造方式，它们的核心大致可以归纳为 两点：1）用的哪种扰动范数球（$\ell_\infty$，$\ell_2$，$\ell_0$）；2）用什么方法在这些范数范围 内优化该扰动。

  • 对抗样本发展时间轴

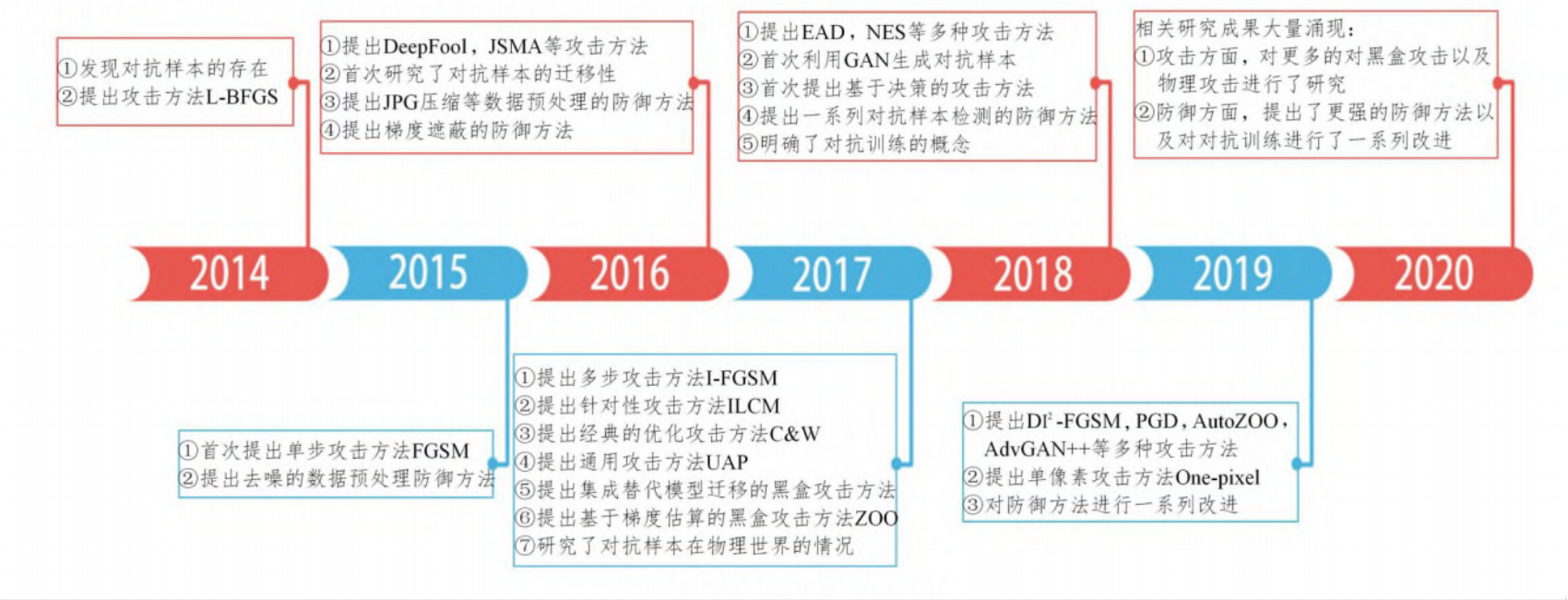
    screenshot

  • 对抗样本构造方法总结

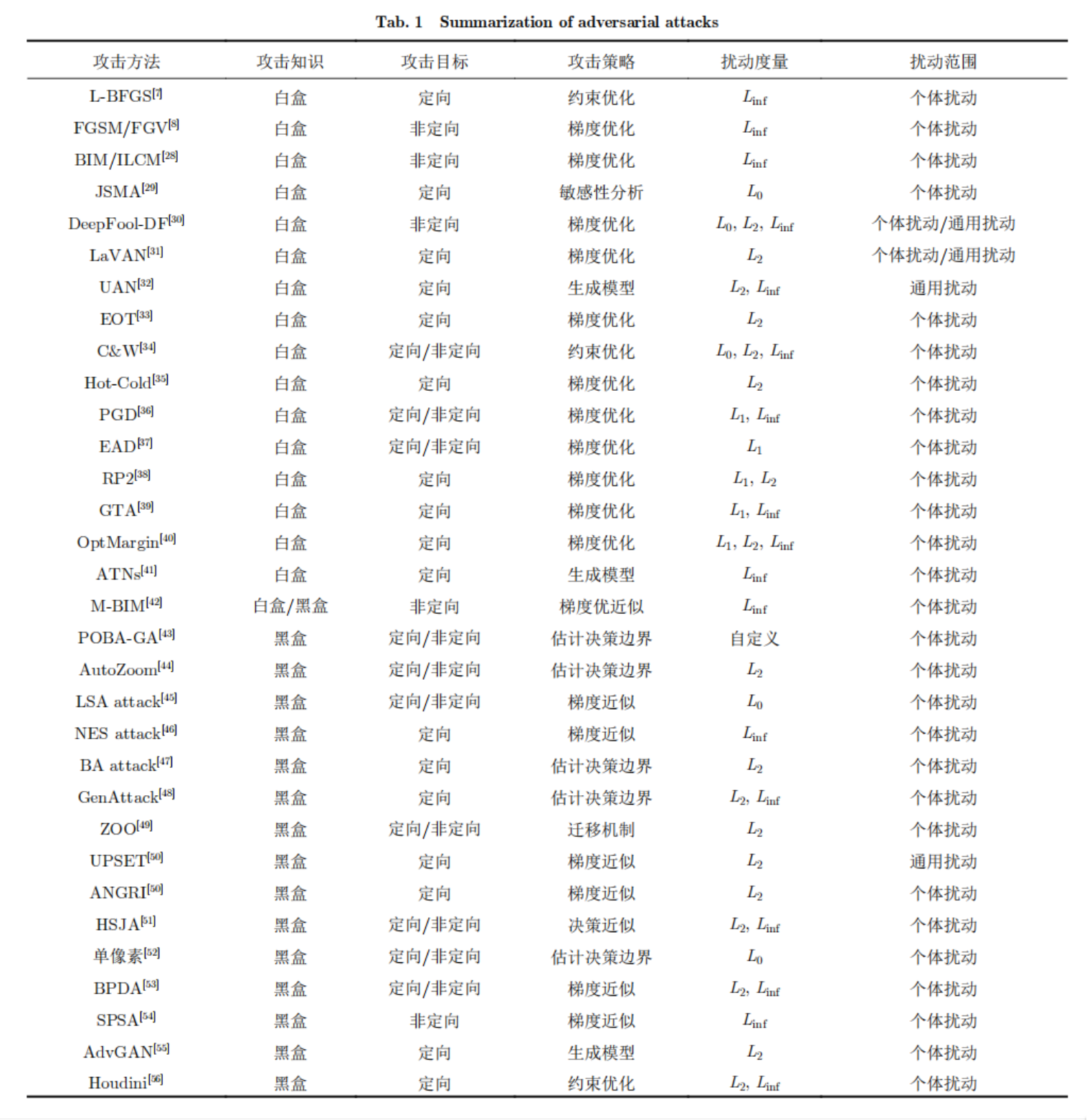
    screenshot

3.对抗训练：增强模型的对抗鲁棒性

应对对抗样本主要有两种策略：

1、设计检测方法，检测到对抗样本后拒绝分类；

2、真正增加模型鲁棒性，使模型正确分类对抗样本。

我们这里主要关注的是第二种策略——增加模型的对抗鲁棒性

3.1求解外部最小化问题

screenshot

回到之前提出的构建对抗鲁棒性模型的表达值，这里值得注意的一点是最大-最小的顺序很重要。

具体的，最大化是在最小化的内部，这意味着攻击方（试图最大化损失）是后手操作（即在得知了模型 信息后再进行攻击）。我们基本上都是假设对手完全了解分类器的参数（这也是之前潜在假设），所以 鲁棒性优化（robust optimization）的目标是即使对手知道模型的全部信息，也能保证模型不被攻击。

对于求解内部最大化问题的三种方法，都有相应的等效方式来训练鲁棒的系统，但是同样的最为主流的的方法还是利用对抗样本进行的对抗训练。

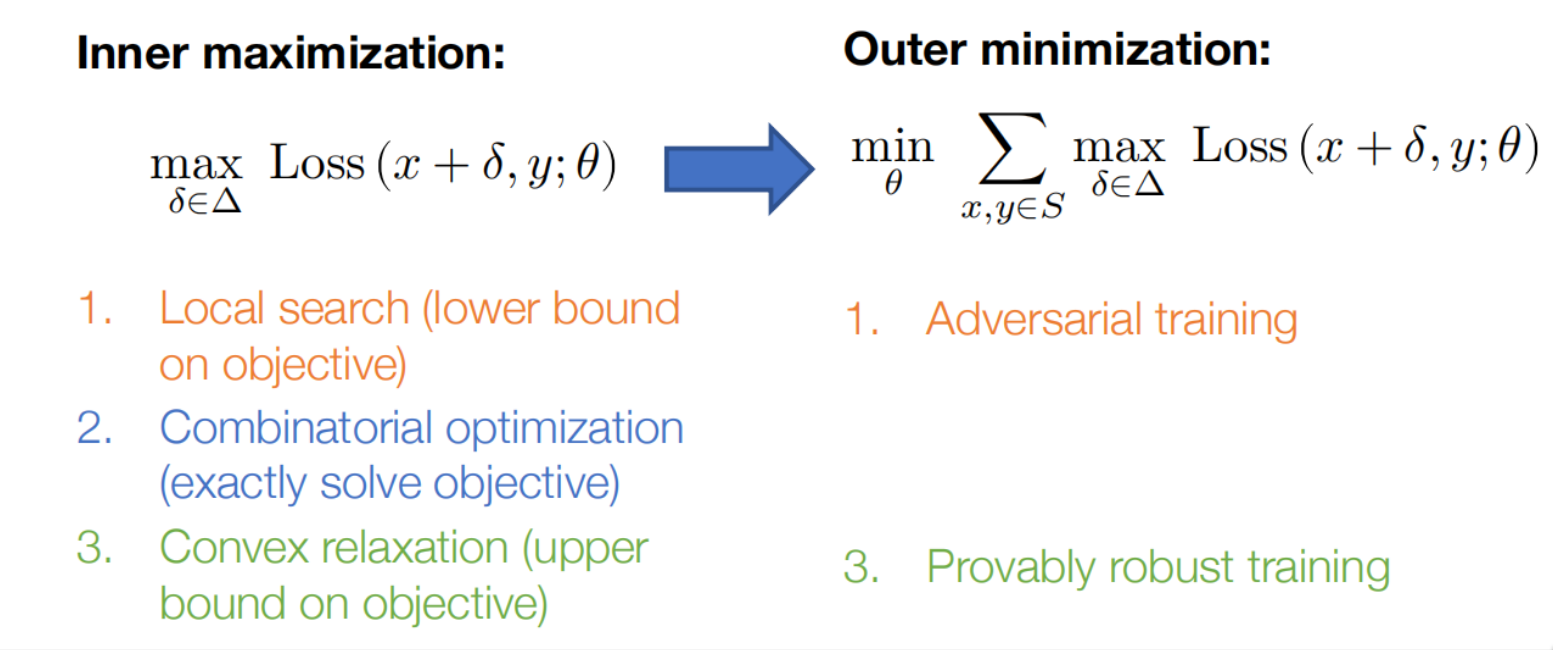
screenshot

3.2对抗训练

这一策略非常简单，就是生成对抗样本，然后将其用于训练，类似一种数据增强的方式。换句话说，因 为标准的训练过程会使得模型容易受到对抗样本的影响，所以我们就用一些对抗样本来训练模型。

假设我们希望使用梯度下降来优化最小-最大目标,例如使用随机梯度下降，只需要在minibatch上迭代计算损失函数关于$\theta$的梯度，并沿负梯度方向 更新，即

\[\theta := \theta - \alpha \frac{1}{|B|} \sum_{x,y \in B} \nabla_\theta \max_{\|\delta\| \leq \epsilon} \ell(h_\theta(x + \delta), y).\]

至于如何计算内部项的梯度，正如我们在前面提到的，只需要利用Danskin’s Theorem：1)找到最大 值；2) 计算在该值下的梯度。即：

\[\DeclareMathOperator*{\argmax}{argmax} \nabla_\theta \max_{\|\delta\| \leq \epsilon} \ell(h_\theta(x + \delta), y) = \nabla_\theta \ell(h_\theta(x + \delta^\star(x)), y)\]

其中，

\[\delta^\star(x) = \argmax_{\|\delta\| \leq \epsilon} \ell(h_\theta(x + \delta), y).\]

Danskin’s theorem成立的前提是我们能够找到最大值。但根据上一部分，我们知道想找到最大值并不 容易，经验上，鲁棒的梯度下降过程和我们求解最大化问题的程度紧密相关，求解得越好，Danskin’s theorem似乎就越接近成立。换句话说，对抗训练的关键是将“强大”的攻击纳入训练过程中。

具体策略如下：

\[% <![CDATA[ \begin{split} & \mbox{Repeat:} \\ & \quad \mbox{1. Select minibatch $B$, initialize gradient vector $g := 0$} \\ & \quad \mbox{2. For each $(x,y)$ in $B$:} \\ & \quad \quad \mbox{a. Find an attack perturbation $\delta^\star$ by (approximately) optimizing } \\ & \qquad \qquad \qquad \delta^\star = \argmax_{\|\delta\| \leq \epsilon} \ell(h_\theta(x + \delta), y) \\ & \quad \quad \mbox{b. Add gradient at $\delta^\star$} \\ & \qquad \qquad \qquad g:= g + \nabla_\theta \ell(h_\theta(x + \delta^\star), y) \\ & \quad \mbox{3. Update parameters $\theta$} \\ & \qquad \qquad \qquad \theta:= \theta - \frac{\alpha}{|B|} g \end{split} %]]>\]

这里需要注意的是对抗训练过程十分耗时，在大规模数据集上的应用受限。鲁棒优化是个min-max问 题，如果我们用10-steps的PGD做对抗训练，那么我们的训练代价就是普通训练的10倍以上。

3.3 评估鲁棒的模型

评估的两种指标

  • robust accuracy：模型在对抗样本上的精度

  • standard accuracy: 模型在干净的样本上的精度

对抗训练领域存在的一个痛点问题——神经网络鲁棒性的提升会伴随着准确率的下降

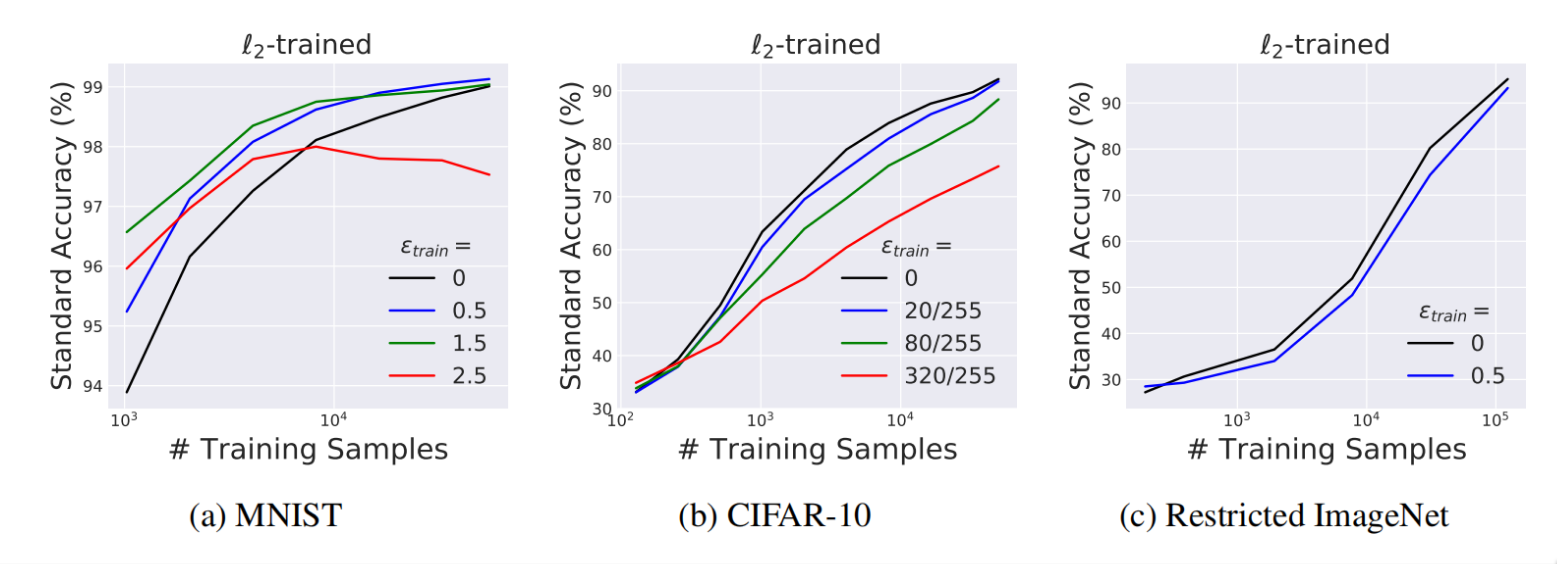
screenshot

4. 对抗鲁棒性的进一步分析

4.1 深度学习为什么不鲁棒？

传统的基于经验风险最小化的神经网络为何不鲁棒？为何需要对抗训练才能使其鲁棒？为什么越鲁棒的 模型，在干净测试集上的精度反而越低？

《Adversarial Examples Are Not Bugs, They Are Features》这篇论文给出了相应的解释

其中作者提出了一种观点：对抗样本不是缺陷，而是特征。对抗脆弱性是我们的模型对数据里易于泛化 的特征过于敏感的直接结果。这里的易于泛化的特征，我们可以把它理解为隐藏在图片像素里的某些模 式（pattern）。

这项工作把特征分成两类：有用且鲁棒的特征$F_{r}$（useful, robust features），有用但不鲁棒的特 征 $F_{nr}$ （useful, non-robust features）。这里的有用指的是能帮助分类器做分类任务的特征。

它认为这两类特征天然存在我们的图像数据集中。虽然我们人类主要是依赖于$F_{r}$做分类任务，我们 人类对$F_{nr}$天然无感。但是我们的深度网络在训练过程中，是竭尽全力地在学习所有有利于减小目 标函数的特征，因此我们的模型会过于依赖这部分有用但是不鲁棒的特征$F_{nr}$ ，而这些不鲁棒的特 征正是导致模型对抗脆弱性的关键：在通常情况下，这些 $F_{nr}$是很有用的，它让模型获得了令人诧 异的泛化性能；然而一旦有敌手通过操纵$F_{nr}$来攻击模型，它就让模型的精度直接降为0，而人类的 精度并不会受到影响。

这篇文章里设计了一个实验。它利用一个现存的鲁棒分类器（经过对抗训练的网络）和一个原始数据集 构造了两个新的数据集：一个数据集仅含有$F_{r}$，另一个数据集仅含有$F_{nr}$，

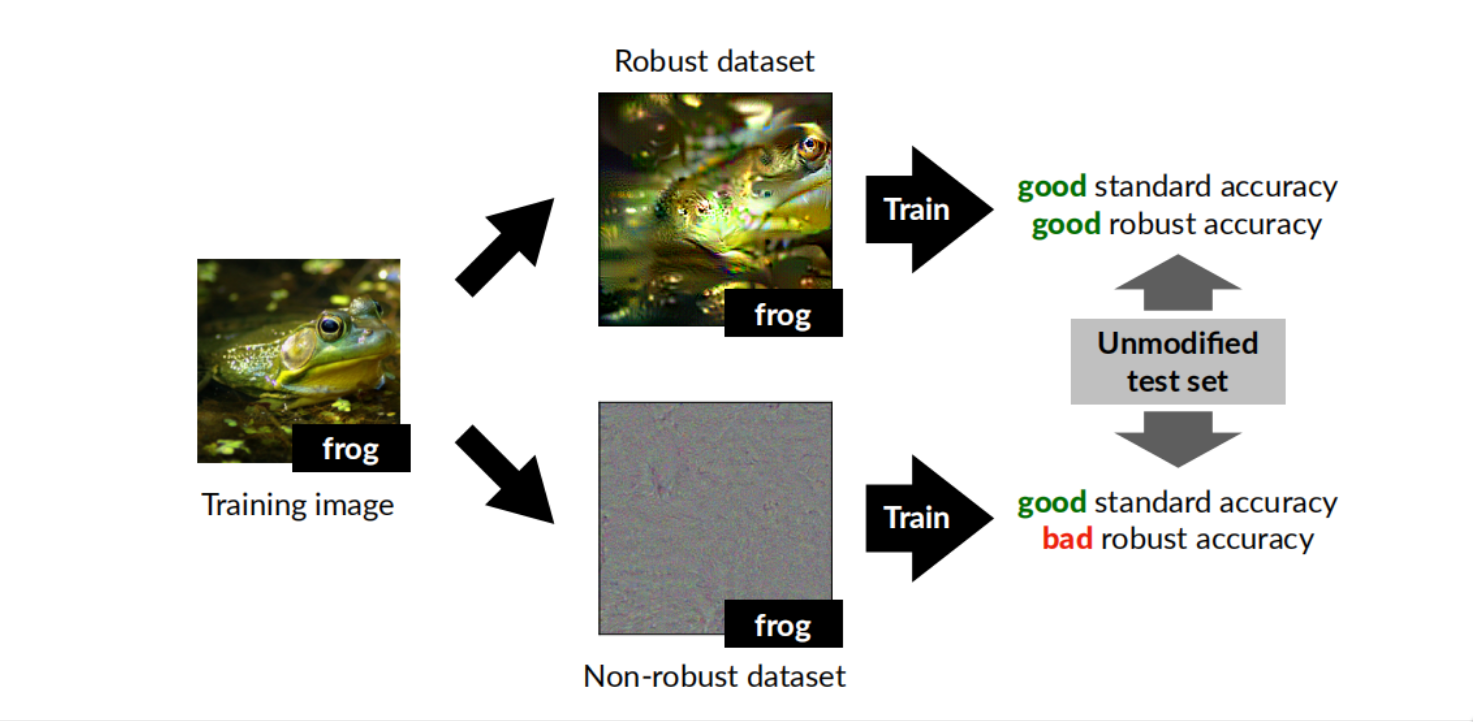
screenshot

实验表明，在一个鲁棒的数据集上普通地训练一个模型，能得到良好的标准精度和鲁棒精度；

而在一个不鲁棒的数据集上普通训练的模型，能有良好的标准精度但是不鲁棒。

这篇文章很好地回答了前面三个问题。模型不鲁棒是因为数据集里存在不鲁棒的特征$F_{nr}$，对抗训 练能够使模型避免依赖 $F_{nr}$，但 $F_{nr}$其实对标准精度有益，所以对抗训练会使得模型的标准精 度下降。

4.2对抗鲁棒性带来的额外益处

对抗训练可以增加模型在测试集上的鲁棒精度（即分类对抗样本的准确率）。通过让模型对人类不敏感 的信号不敏感，鲁棒的训练目标可能会使得模型学习到更类似我们人脑使用的特征表示。这种与人类感 知更相符的特征表示，会有一些额外的益处。

  • 可解释性：鲁棒模型对输入的梯度比普通模型更加有意义

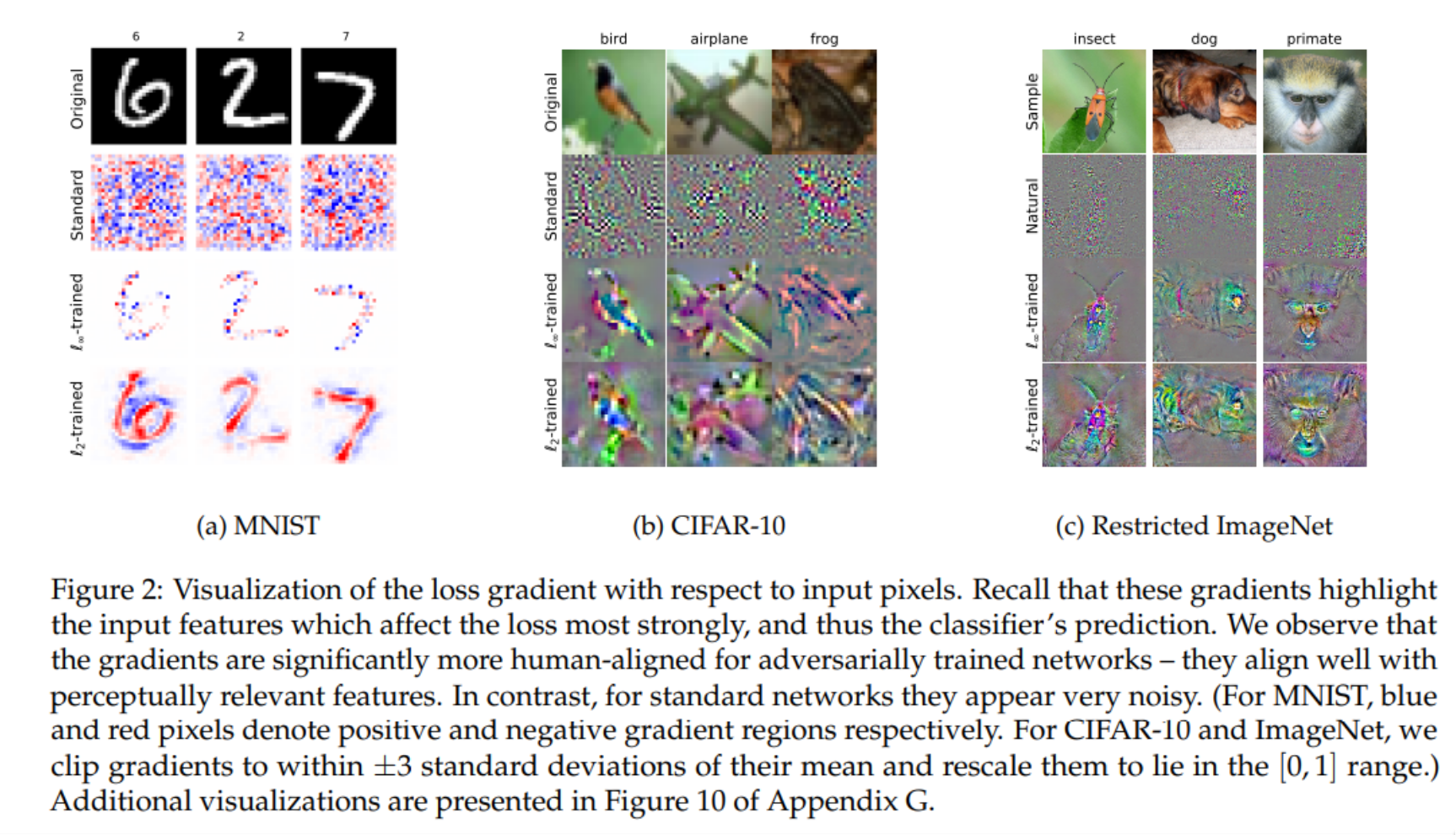
    screenshot

    Robustness May Be at Odds with Accuracy, ICLR 2019

  • 图像合成：利用一个鲁棒的分类器可以做许多从前只有生成模型可以做的图像合成任务

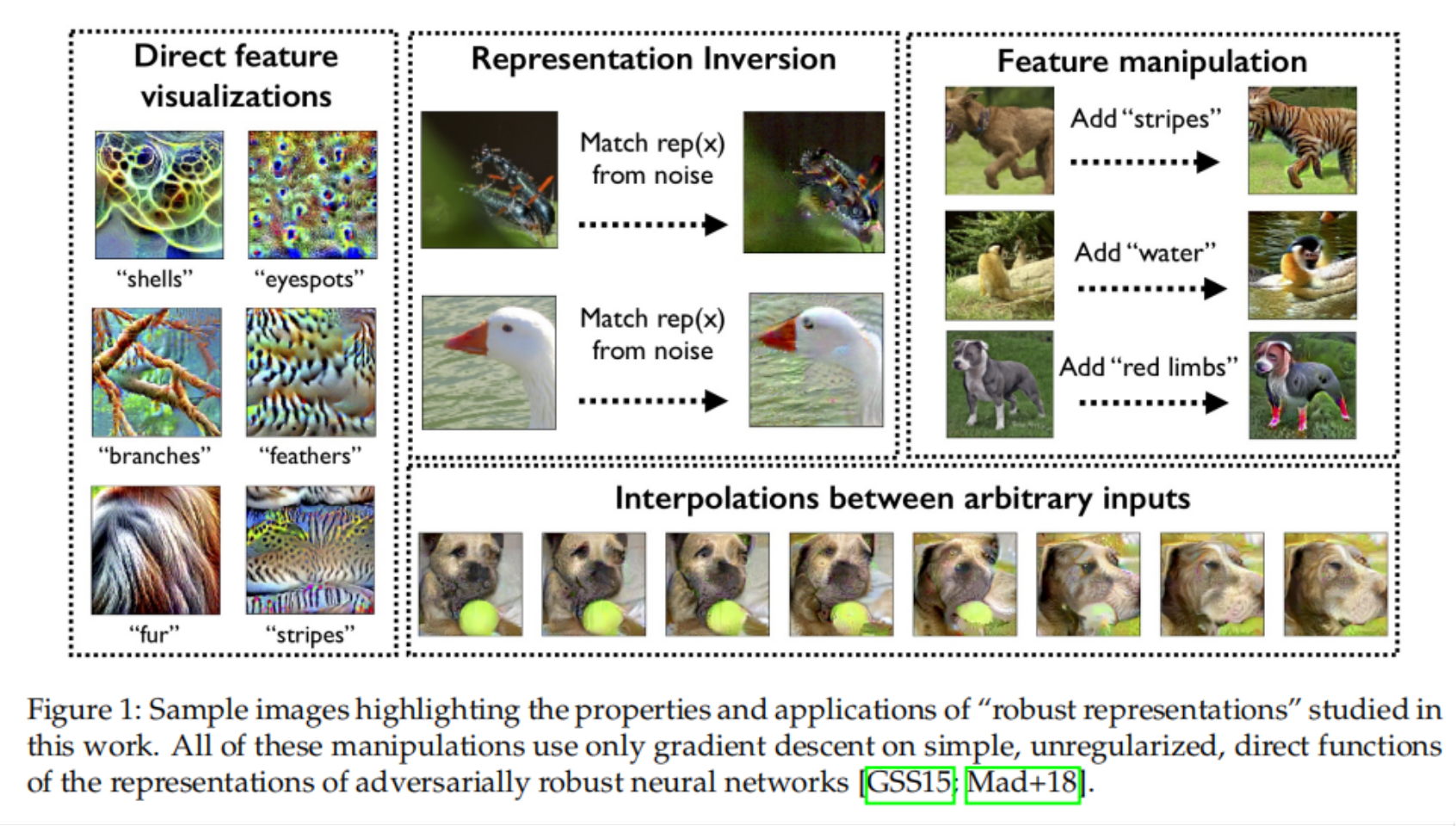
    screenshot

    Adversarial Robustness as a Prior for Learned Representations 2019

  • 异常检测：对抗鲁棒性可以增加异常检测的性能

  • 迁移学习：对抗鲁棒的预训练模型迁移到新任务时具有更好的性能

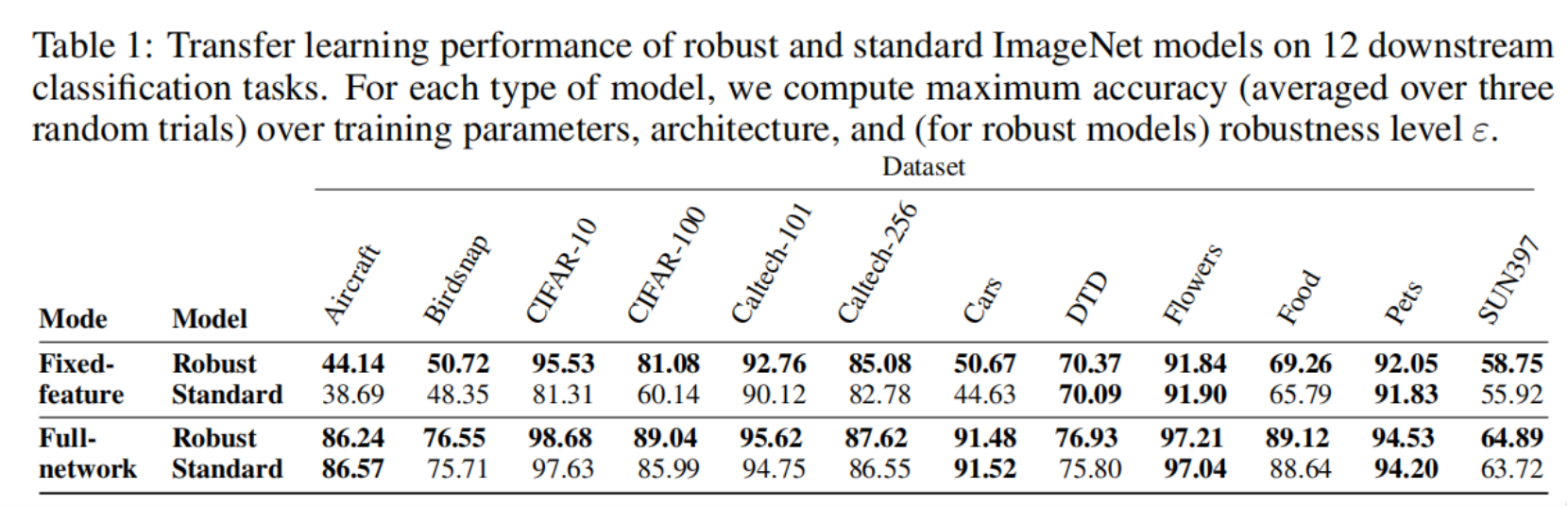
    screenshot

    Do Adversarially Robust ImageNet Models Transfer Better?2020

  • ……

Reference

Breaking neural networks with adversarial attacks

Adversarial Robustness - Theory and Practice

对抗鲁棒性简介 - 王晋东不在家的文章 - 知乎 https://zhuanlan.zhihu.com/p/211304103

Notes:

Tutorial materials