数据是人工智能的燃料,优秀的深度学习模型需要依靠大量高质量数据集进行训练。然而,随着模型精度的不断提升,对于个人隐私的泄露现象也变得越发严重。此外,随着互联网企业的扩展,用户数据开始担任重要生产资料的角色,成为各大垄断企业的护城河。欧盟,作为反对互联网垄断的桥头堡,同时也作为隐私保护的急先锋,在2018年正式施行法案《通用数据保护条例》(General Data protection Regulation, GDPR)。GDPR主张个人对数据的四项权利,请求权,拒绝权,修正权和删除、遗忘权。请求权,即个人有权了解其个人数据是否被处理,哪些个人数据以怎样的方式被处理以及进行了哪些数据处理操作;拒绝权,即个人有令人信服的合法理由,可禁止进行某些数据处理操作,比如个人可拒绝以营销为目的的个人数据处理。遗忘权,即个人有权寻求删除其个人数据的影响,比如用个人的微博,抖音数据训练的推荐算法,能够把个人的影响给忘掉。此外,GDPR还对数据的传输有明确的要求,比如欧盟境内的数据不得在境外被使用。
那么,一个自然的问题是,如何让人工智能模型的训练过程能够符合数据保护条例,保护个人隐私呢?依据GDPR的要求,首先数据的存储必须满足去中心化,而模型则需要在去中心化的数据库上进行分布式训练。联邦学习[1]是应对这种要求的解决方案,它允许模型在本地数据库上训练,并构建一个全局的调度器,通过对不同本地模型的更新进行汇总(即FedAvg算法),获得全局模型。得到的全局模型能够利用所有本地数据的信息,并得到更好的模型精度。其次,GDPR要求个人能够控制其数据对于模型的影响。人工智能模型是通过归纳所有数据信息构建的,它的输出结果是否会泄露个人隐私呢?差分隐私(Differential Privacy)系统地探讨并解决了这一问题。差分隐私因其具有强大的数学理论支撑而被广泛认为是隐私保护的黄金标准。为了缓解机器学习中的隐私问题,许多研究工作对具有差分隐私保证的机器学习进行了研究。
这个教程由两位来自微软亚研院的Huishuai Zhang 和 Wei Chen研究员主讲,主要涵盖差分隐私方法及其性质、隐私的机器学习以及机器学习中的差分隐私方面的内容,教程中对于通过加密来保障数据安全方面的技术仅做概要式介绍。在本篇博客中,我们将对该分享进行详细的介绍,总结与提炼,并在关键处做必要的补充分析。
本文由本人及浙江大学CAD国家重点实验室可视分析与可视智能小组(VAI)博士生FengHZ合作整理完成,未经作者同意禁止转载。
隐私背景
该部分简要的介绍了从一般层面和机器学习层面上的隐私定义,以及在机器学习中隐私问题的必要性,并且简要的概述了机器学习三个主要阶段中较为主流的保护隐私的方法。
隐私的定义
tutorial中提到,维基百科中将隐私定义为:隐私权是指个人(团体或机构)自行决定何时、如何以及在多大程度上向他人传达其相关信息的权利,这是关于隐私的一般性定义;同时机器学习中将隐私定义为:机器学习中的数据隐私保护,即在使用数据的同时保护个人隐私偏好和身份信息的完整性。
信息隐私 ( Privacy ):指的是当一个组织内敏感数据被拥有权限的人员所使用于某些技术、过程 ( 如数据分析、训练模型 ) 时,对数据敏感信息进行保护的过程与规则。
数据的隐私 ( Privacy ) 与安全 ( Security ) 并不等价:有的时候很多人提到数据隐私时,会与数据安全混为一谈,但其实两者并不等价。数据安全通常指防止数据被非法访问;而数据隐私则一般指在数据被合法访问时,防止其中的敏感信息被访问者以某些方式”逆向”获取,避免因数据被”逆向”推导出而造成的敏感信息泄露和滥用。
以下对“什么是隐私”这一问题进行更为深入的讨论。在不同的考量下,隐私的定义也不一样。目前普遍比较接受的定义是:“单个用户的某一些属性” 可以被看做是隐私。注意该说法所强调的是“单个用户”,也就是说,如果是一群用户的某一些属性,那么可以不看做隐私。譬如,医院发布调查报告说,抽烟的人会有更高几率得肺癌,这个不泄露任何隐私。但是如果医生说,张三因为抽烟,所以有\(x\%\)的概率得肺癌,这就是个人隐私的泄露。如果我们拥有一个数据库,那么对精确的个体信息的查询与检索都会泄露隐私,因此对于个人数据的加密是最基本的保护隐私策略。然而,就算我们对个人数据进行了加密,对一群用户的某些属性的查询,以及对查询结果进行加工与建模,也就是“数据分析”,往往也会泄露个人隐私。而相比于数据加密,对数据分析的过程进行隐私保护因其不对称性更加具有难点,因为数据加密过程中,解密者与攻击者往往是两方,但是数据分析的过程中,分析师与“隐私攻击者”则是一方。
我们先来举几个例子,看看什么样的数据分析行为会侵犯隐私,以及什么样的行为看似不会侵犯隐私,但是通过一连串叠加也会侵犯个人隐私。首先,在直觉上,如果查询的数据库特别大,而且我们规定只允许查询摘要形式的信息或者统计形式的信息,这种数据分析方法看起来保护了个人隐私。但是,如果我们知道某个个体的信息包含在数据库中,我们就可以利用一种叫差分攻击的方法得到个体的信息。比如,如果我们已知X的信息在某个大型医疗数据库中。那么我们可以查询:有多少人患血友病,以及条件查询,有多少个不叫X的人患白血病。这样经过差分,我们就得到了X是否患血友病的信息。对于这种情况,如果我们引入某种监督机制,比如有一个监督者禁止这种不安全的查询,或者有监督者在必要的时候对数据库进行匿名处理,似乎可以避免上述的差分攻击,是否有一个监督机制能保证数据分析过程中,隐私不被泄露吗?答案是没有,原因有二:(1) 禁止查询的决定本身也会带来隐私泄露。比如国家不公布第七次人口普查数据,或者从2006年开始不公布中国的基尼系数,这本身也有某些信息。(2) 可以将单次破坏隐私的查询拆分成一系列查询,而对于每次查询,很难判断是否破坏隐私。最后,由于数据分析师的先验知识背景非常多样,因此数据分析师的辅助信息也会将一些不破坏隐私的查询变得破坏隐私,这就带来了第二种隐私泄露的形式,即由于数据库之外的辅助信息带来的隐私泄露。比如我们知道邻居X在某一天去了医院,而我们得到的匿名医院数据库中,在这一天的数据条目特别少,那么X的个人信息也会以某种高概率泄露。比如作为X的邻居,我们发现他常常去买蛋糕。但是有一段时间他忽然开始买不含糖的面包了,如果我是一个医生,我可能会猜想他患了糖尿病,这就是辅助信息带来的隐私泄露。
综上所述,差分攻击与辅助信息是数据分析过程中隐私泄露的主要诱因,而引入监管也不能保证隐私。针对这种状况,差分隐私提出了一种数据分析过程的隐私保护定义,即对于数据库数据的任何分析,以及根据分析结果与其他信息进行的进一步的合并加工,都不会泄露个人隐私。
ai中隐私保护的必要性
ai中的隐私保护主要有以下四点的必要性,(1)敏感的数据随时随地都会被记录下来,比如大多数人随身携带的智能手机,是一个非常强大的感知工具,它不断地共享有关用户的位置,数字和物理交互等方面的数据;(2)机器学习是一个提取信息的强大工具,即算法模型在某种意义上它们会持续性的过拟合特定的训练样本,即训练样本被其隐式记忆(3)AI使得对手能够利用数据,比如一些攻击方法能够通过分析模型内部参数或反复访问查询不透明的模型来收集数据,从而能够恢复隐私敏感的训练数据。(4)简单的匿名技术是不安全的,互联网行业搜集信息的出发点:一、收集用户信息是必要的,这样有助于改善产品或服务。二、匿名收集用户信息的,并不保存任何用户的身份信息。但事实上匿名并不能完全保证用户的隐私安全,经典的案例为,Netflix 曾放出“经过匿名处理的”上亿条电影评分数据,“仅仅保留了每个用户对电影的评分和评分的时间戳”,希望通过竞赛的形式,找到更好的影片推荐算法。但是 2009年,德州大学的两位研究人员,通过这些匿名数据与公开的IMDB数据做对比,成功将匿名数据与具体的用户对应了起来。
那么应该怎样对机器学习模型进行保护呢?
隐私保护关键技术概述
机器学习中隐私保护的核心原则为控制从隐私到公开这个过程的信息流
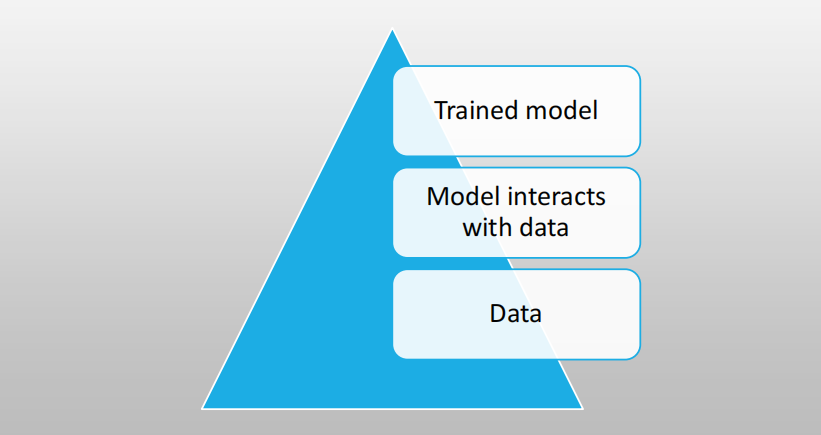
模型与数据交互的部分有如上图所列的三块,首先是原始数据,其次是和数据交互的模型,以及训练完成的模型,也就是说模型隐私的泄露大体上是在这三个过程中发生。这三块对应隐私保护计算架构体系中三个逻辑角色:数据方、计算方和结果方。数据方是提供数据的组织或个人,计算方是提供算力的组织或个人,结果方是接收结果的组织或个人。
- 数据:即保护原始数据的安全,主要是在数据存储、数据库层面上保障数据安全。数据静态存储和数据传输的安全防护技术已经比较成熟,比如访问控制、存储加密、传输加密、内容审计等。而隐私计算保护,则专注于数据计算过程和计算结果的隐私保护。
- 和数据交互的模型:解决方案主要有联邦学习、同态加密、多方计算以及受信任的执行环境
- 训练完成的模型:训练好的模型一样会泄露隐私,主要的解决方案为差分隐私
接下来将会简要的概述隐私保护几个解决方案,包括联邦学习,以及基于加密计算的同态加密、安全多方计算和受信任的执行环境,还有本次tutorial的重点差分隐私
联邦学习
随着大数据的进一步发展,人们希望由算法和大数据驱动的人工智能广泛使用于各个领域(如AlphaGo以30万棋局作为训练数据)。但是,大多数领域数据有限、质量较差,如医疗领域需要医生标注数据,但是医生时间有限;而且数据源以孤岛形式存在,难以整合数据,如产品推荐系统中销售方和平台、用户的数据壁垒如何在满足用户隐私保护、数据安全和政府法规的前提下,进行跨组织的数据合作是困扰人工智能从业者的一大难题。而“联邦学习”将成为解决这一行业性难题的关键技术。
联邦学习(Federated Learning,FL)最初由Google提出,用于解决由一个中央服务器协调众多分散的智能终端实现语言预测模型的更新,是一种解决数据孤岛的机器学习策略,依据GDPR的要求,首先数据的存储必须满足去中心化,而模型则需要在去中心化的数据库上进行分布式训练。联邦学习是应对这种要求的解决方案,它允许模型在本地数据库上训练,并构建一个全局的调度器,通过对不同本地模型的更新进行汇总(即FedAvg算法),获得全局模型。得到的全局模型能够利用所有本地数据的信息,并得到更好的模型精度。
加密计算
加密计算保证了数据是在ML系统中被加密计算的,加密计算当前的解决方案包括受信任的执行环境、同态加密以及多方计算
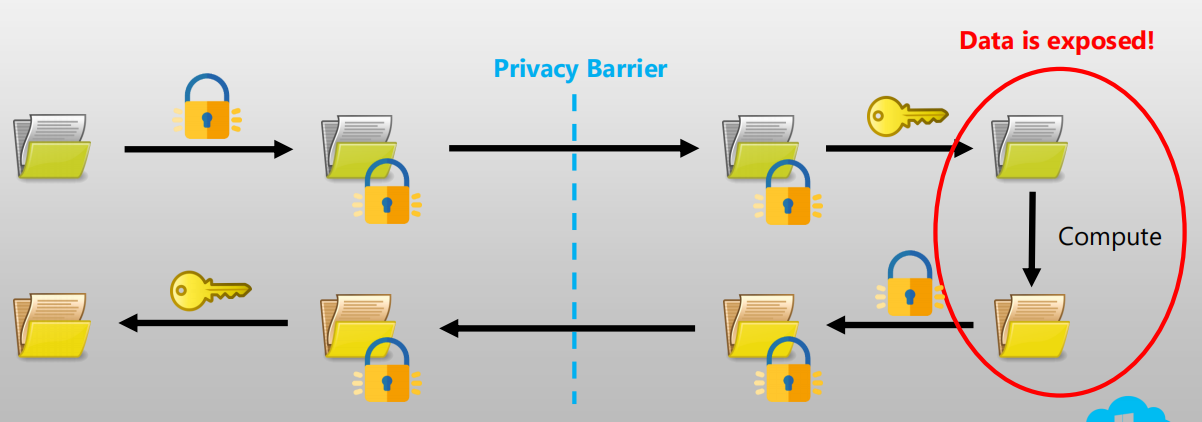
(1)可信执行环境
机密计算是基于硬件可信执行环境(Trust Execution Environment)实现数据和应用保护的技术,Gartner也将其称为Enclave(借助政治上的“飞地”概念)。其核心思想是以可信硬件为载体,提供硬件级强安全隔离和通用计算环境,在完善的密码服务加持下形成“密室”,数据仅在“密室”内才进行解密并计算,除此之外任何其他方法都无法接触到数据明文内容。基于软件的 TEE的例子为Windows 中的虚拟安全模式 (VSM),而基于硬件的TEE有IntelSGX。
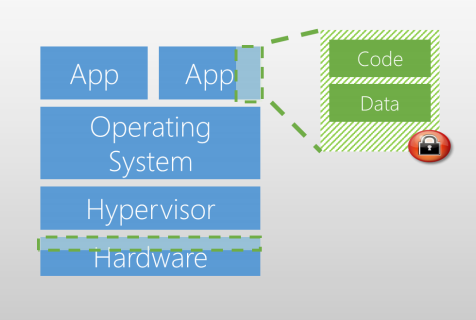
[Ohrimenko et al. 2016, Hunt et al. 2018]
(2)同态加密
同态加密(Homomorphic Encryption, HE) 是指满足密文同态运算性质的加密算法,即数据经过同态加密之后,对密文进行特定的计算,得到的密文计算结果在进行对应的同态解密后的明文等同于对明文数据直接进行相同的计算,实现数据的“可算不可见”。
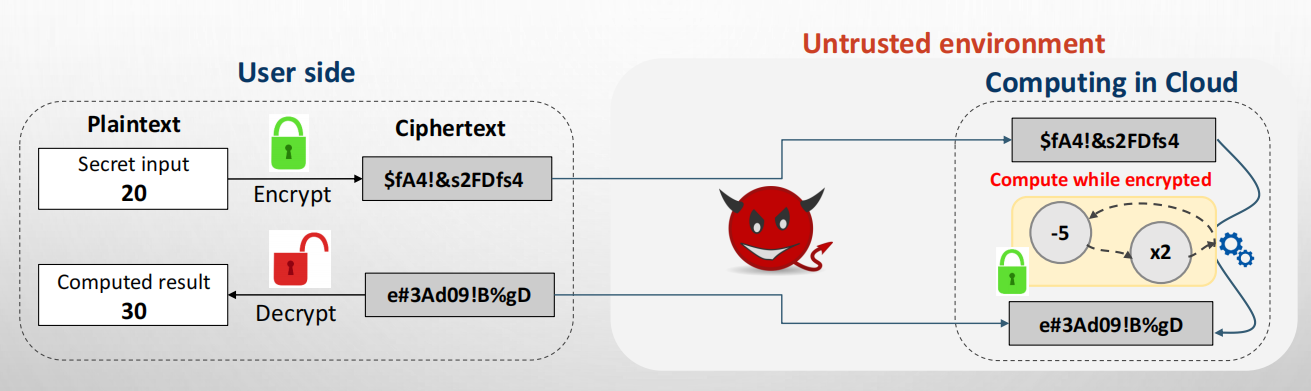
关于这个方法好的一方面是:非常强大的安全保障;不好的一方面是:非常大的性能损失 (~100-100,000x);只支持部分计算
(3)安全多方计算
安全对方计算(Secure Multi-Party Computation,SMPC)最初由图灵奖获得者姚期智院士提出,用于解决“百万富翁问题”的一个算法设想。安全多方计算解决的是一组相互不信任的参与方各自拥有秘密数据,协同计算一个既定函数的问题。参与方除了获得计算结果,无法获得之外的任何信息。在整个计算过程中,参与方拥有对自身数据的绝对控制权。
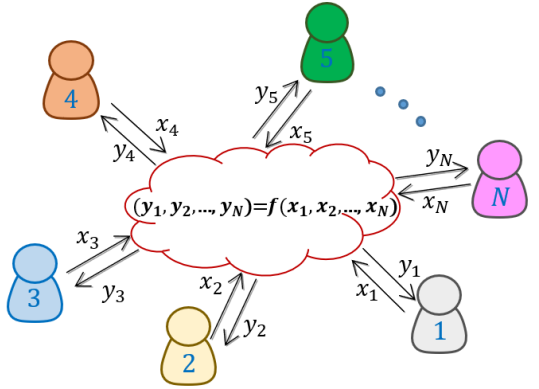
安全多方计算逻辑架构:同一个分布式网络中,有n个参与方\(P_1,P_2,P_3,…,P_n,\)各自拥有自己的秘密数据\(x_i(i=1,2,3,…,n)\),它们共同执行既定的函数\(y=f(x_1,x_2,x_3…,x_i)\),y为Pi的执行结果。\(P_i\)除了\(y_i\)得不到任何其他信息。目标为通过隐私输入,联合计算函数输出,例如多个数字的总和,百万富翁问题。该方法具有巨大通信开销的问题。
差分隐私
训练好的模型一样会泄露隐私,主要的解决方案为差分隐私,它具备严谨的数学理论,其核心优点在于:能够实现和背景知识严格无关的隐私保护模型,理论了上可以抵御任何攻击,并且差分隐私模型建立在严格的数学理论基础上,对隐私保护提供了量化的评估方法和严谨的数学证明
差分隐私当前最主要的实现方式是在结果集中添加噪声,解决单个查询的隐私保护问题。添加噪声带来的问题是噪声对模型可用性影响,如何能够在安全性与可用性上找到平衡,是差分隐私的重点研究方向。
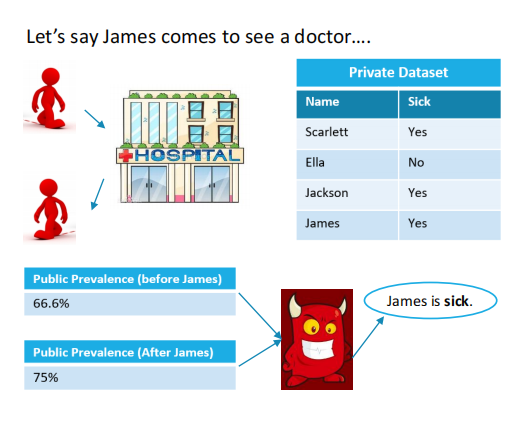
如下图的例子,有一个医院,医院中的病患记录为隐私数据,原本一共有三条的病患记录,记录中有两人患病的一人未患病,当有一个叫做James的人去这个医院看病,James看病之前患病率为2/3*110%=66.7%,James看病之后患病率变成了3/4 *110%=75%,于是可以从外部推断,James是患病的,于是James的隐私就被泄漏了。
而差分隐私的机制为向查询结果添加噪声,使得原本确定的查询结果2和3变成了一个随机概率分布的变量,现在,如果James不在这个医院的数据库和James在这个医院的数据库得到的结果都接近于70.8%(前两个患病率的平均),即两个数据集查询得到某一个结果的概率很接近,以至于我们根本分不清这个结果来自于哪一个数据集,这样也就实现了外部攻击者的知识不会因为James的出现与否而发生变化。
差分隐私方法
这一章节将介绍差分隐私的核心概念和性质,以及差分隐私的变体Rényi差分隐私,是之后相关方法的理论基础。
差分隐私
在给出差分隐私的精确定义前,我们需要对随机算法进行一些定义。
定义1. (概率单纯形) 给定一个数目有限的离散集\(\mathcal{O}\),我们可以将\(\mathcal{O}\)看作是有限数量的互斥事件,定义\(\mathcal{O}\)上的概率单纯形为\(\Delta(\mathcal{O})\),满足 \(\Delta(\mathcal{O})=\{\mathbf{x}\in\mathbb{R}^{\vert \mathcal{O}\vert}:x_i\geq0 \text{ and }\sum_{i=1}^{\vert \mathcal{O}\vert}x_i=1\}\)
概率单纯形其实就是在事件集\(\mathcal{O}\)上所有可能的概率分布的集合,而每一个元素\(\mathbf{x}\in \Delta(\mathcal{O})\)就是一种可能的概率分布。基于概率单纯形,我们可以对随机算法进行如下的形式化定义:
定义2.(随机算法) 记数据库中所有条目的集合为\(\mathcal{X}\),则所有可能的子数据库构成的空间为\(\mathbb{N}^{\vert \mathcal{X}\vert}\)。随机算法\(\mathcal{M}\)将一个子数据库\(D\in \mathbb{N}^{\vert \mathcal{X}\vert}\)映射到离散集合\(\mathcal{O}\)的概率单纯形的一个可能分布上,即 \(\mathcal{M}:\mathbb{N}^{\vert \mathcal{X}\vert}\rightarrow \Delta(\mathcal{O})\)
我们也称\(\mathcal{O}\)为随机算法\(\mathcal{M}\)的 Range,即\(\text{Range}(\mathcal{M})=\mathcal{O}\)。其中对于每一个可能作为算法输入的数据库\(D\),随机算法\(\mathcal{M}\)先将其映射到一个概率分布,即对于任意\(D\in \mathbb{N}^{\vert \mathcal{X}\vert}\),以及任意的\(o\in \mathcal{O}\),随机算法\(\mathcal{M}(D)\)以\((\mathcal{M}(D))_{o}\)的概率输出结果为\(o\)。
如何直观地理解随机算法呢?在数据分析过程中,\(\mathcal{M}\)可以是某种模糊查询方法。比如查询一群人的平均工资范围(如\(1k-2k,2k-3k,>3k\)),直接查询方法对输入的数据进行加和求均值,然后输出该均值对应的范围,而随机算法则是对均值再加一个噪声,然后输出加噪后结果对应的范围,这样如果工资均值是1900,噪声服从\(N(100,10)\)的正态分布,那么其回答将会大概以\(49.3\%\)的概率回答\(1k-2k\),以\(50.7\%\)的概率回答剩下的选项。\(\mathcal{M}\)还可以是从原始数据库到合成数据库的映射,然后输出合成数据库中的查询结果,比如对原始数据库中的工资水平构建分布模型,然后从分布中采样生成相同大小的新数据库,并输出新数据库中的结果;\(\mathcal{M}\)也可以是一系列输出为概率分布的机器学习算法,以机器学习中的图像分类问题为例,此时\(\mathcal{M}\)通过带标注的图像数据库\(D\)进行训练,并对未知的图像进行预测,预测结果为分类概率。
有了随机算法,我们还需要定义数据库之间的距离。一般用\(l_1\text{-norm}\)表示数据库之间的距离。对于两个数据库 \(D,D'\in \mathbb{N}^{\vert \mathcal{X}\vert}\),我们定义它们的\(l_1\)距离\(\Vert D-D'\Vert _1\)为两个Database中不同的记录的个数。如果\(\Vert D-D'\Vert _1=1\),我们就称\(D,D'\)为相邻数据集(Neighboring Datasets),此时\(D,D'\)只相差一个记录。
定义
差分隐私是一种严格可证明的数学框架,其基本思想是对原始数据转换或对输出结果添加噪声来保护数据隐私,确保数据集中任何单个记录的修改都不会对统计结果造成显著的影响。差分隐私可以直观理解为,对于两个相似的Database,要求随机算法在两个Database上的表现也相似,它的形式化定义如下:
差分隐私的形式一:严格的差分隐私
定义3.(\(\epsilon\)-差分隐私) 我们称\(\mathbb{N}^{\vert \mathcal{X}\vert}\)上的随机算法\(\mathcal{M}\),如果\(\epsilon\text{-differentially private}\)对于所有的随机事件\(\mathcal{S}\subset \mathcal{O}\),以及对于所有的相邻数据库\(D,D'\in \mathbb{N}^{\vert \mathcal{X}\vert}\),满足 \(\frac{\operatorname{Pr}[\mathcal{M}(D) \in S]}{\operatorname{Pr}\left[\mathcal{M}\left(D^{\prime}\right) \in S\right]} \leq e^{\varepsilon}\)
其中参数\(\varepsilon\)为隐私保护预算(可以看做是能够接受的隐私泄露量),用于控制随机算法\(\mathcal{M}\)在邻近数据集上获得相同输出的概率比值,反映了算法\(\mathcal{M}\)的隐私保护水平,ε越小,隐私保护水平越高
差分隐私的形式二:松弛的差分隐私
上面定义的差分隐私太过严格,在实际的应用中需要很多的隐私预算。因此为了算法的实用性,后面引入了松弛版本的差分隐私,定义如下:
定义4.(\((\epsilon,\delta)\)-差分隐私) 我们称\(\mathbb{N}^{\vert \mathcal{X}\vert}\)上的随机算法\(\mathcal{M}\)满足\((\epsilon,\delta)\text{-differentially private}\),如果对于所有的随机事件\(\mathcal{S}\subset \mathcal{O}\),以及对于所有的相邻数据库\(D,D'\in \mathbb{N}^{\vert \mathcal{X}\vert}\),满足 \(\text{Pr}[\mathcal{M}(D)\in \mathcal{S}]\leq \exp(\epsilon)\text{Pr}[\mathcal{M}(D')\in \mathcal{S}]+\delta \tag{1}\)
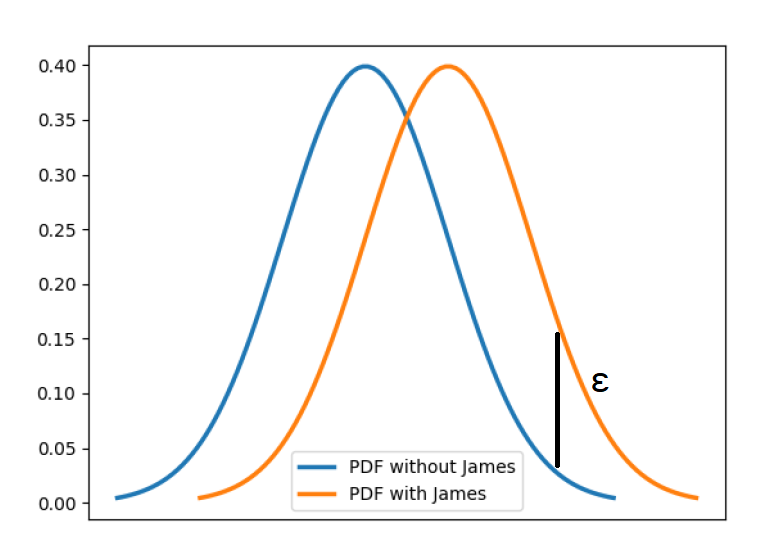
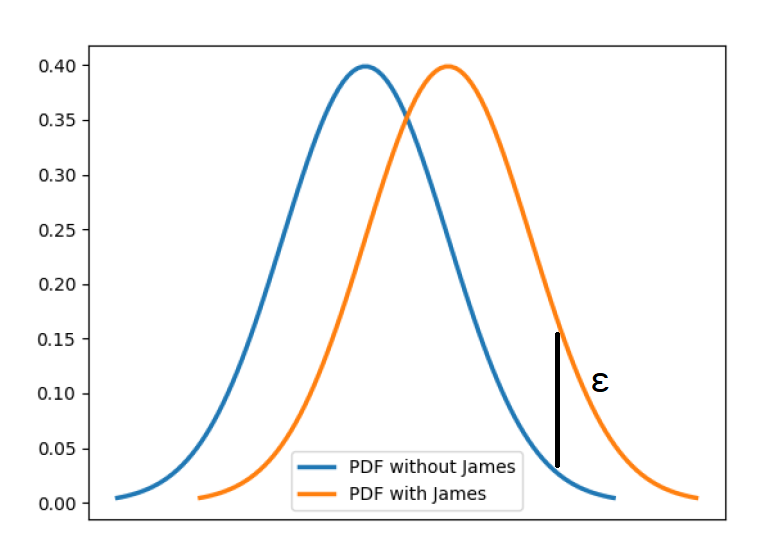
将定义4进行等价变换\(\frac{\operatorname{Pr}[\mathcal{M}(D) \in S]-\delta}{\operatorname{Pr}\left[\mathcal{M}\left(D^{\prime}\right) \in S\right]} \leq e^{\varepsilon}\)即在定义3中的约束不等式\(\frac{\operatorname{Pr}[\mathcal{M}(D) \in S]}{\operatorname{Pr}\left[\mathcal{M}\left(D^{\prime}\right) \in S\right]} \leq e^{\varepsilon}\)的分子处引入了表示违背差分隐私的概率的松弛项\(\delta\),下图展示了对应的直观理解,也就是说我们可以容忍一个较小的差距。
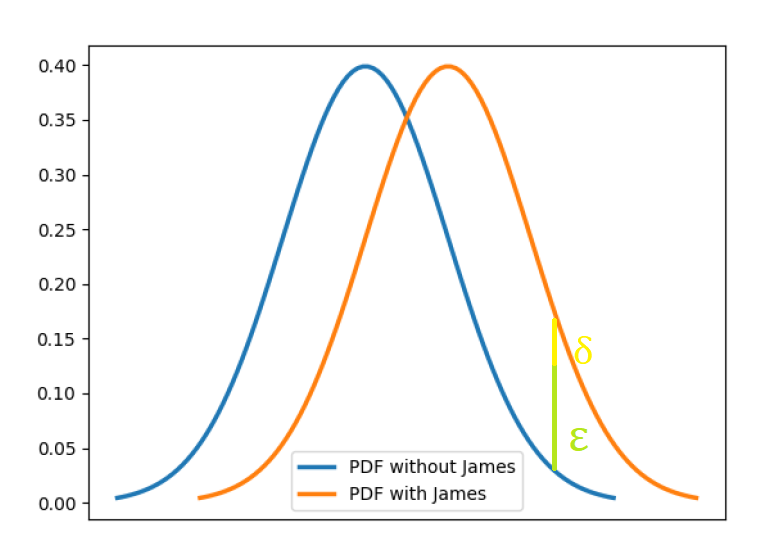
那么差分隐私又是怎样和隐私保护相关联的呢?通过下图来直观的解释一下,上下两个相邻数据集为算法的输入,其中只相差一个用户的数据,即其中绿色的部分。当算法的输出结果相近或相同的情况下就很难通过输出结果来判断输入的数据集是这两个中的哪一个,也就不可能得知是否包含绿色用户的隐私信息,这种情况下就保护了这个用户数据的隐私。
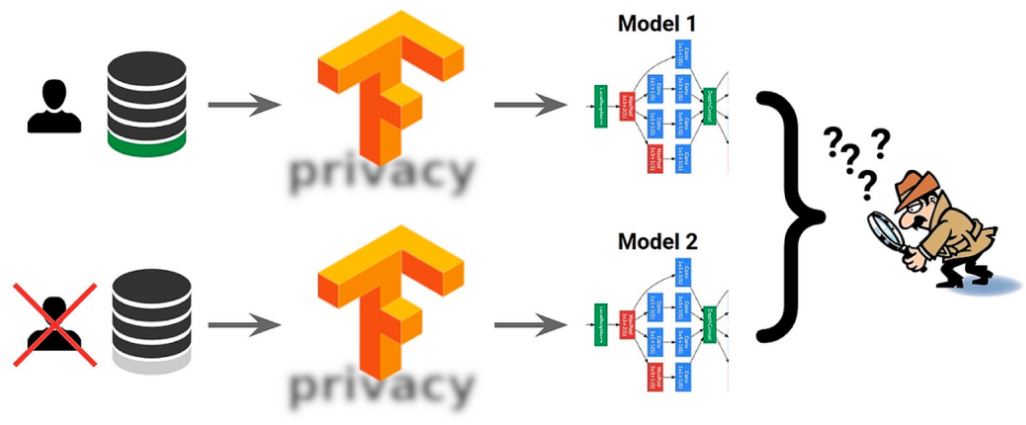
而上面的差分隐私的定义不等式对于所有可能相邻数据集都成立,这意味着无论输入的数据中相差的是哪一个用户的数据,都无法通过输出结果获得其输入的数据集,这样就实现了对用户数据的隐私保护。
敏感度
差分隐私保护可以通过在查询函数的返回值中加入适量的干扰噪声来实现。加入噪声过多会影响结果的可用性,过少则无法提供足够的安全保障。此外,噪声对于数据集的影响还和数据集本身以及所使用的查询算法有关。譬如说一个数据集中的样本都比较相似,那么去掉一两条数据也并不会对查询造成巨大的影响。此外,如果我们使用的查询算法都是概率查询,譬如分类问题,那么查询的差异就可以控制在范围\(1\),而如果查询的是工资的范围,那么查询差异就会很大。基于这种动机,引入敏感度这一参数,它指删除数据集中任一记录对查询结果造成的最大改变,是决定加入噪声量大小的关键参数,定义如下:
定义5.(敏感度) 设有函数\(f: D \rightarrow R^{d}\), 输入为某子数据库\(D\in \mathbb{N}^{\vert \mathcal{X}\vert}\),输出为\(d\)维实数向量。在所有的相邻数据库\(D,D'\in \mathbb{N}^{\vert \mathcal{X}\vert}\)上定义敏感度 \(\Delta_{f}=\max _{D, D^{\prime}}\Vert f(D)-f\left(D^{\prime}\right)\Vert\) 其中,\(\left \| f(D)-f(D') \right \|\)是两个向量之间的距离,常用距离为\(L1,L2\)。函数的敏感度由函数本身决定,不同的函数有不同的敏感度。结合定义理解,敏感度就是一个函数/算法f在相邻数据集上输出的最大的距离,并且这个距离通过L1或者L2范数来衡量,体现了每一个用户对输出所能造成的最大影响。
噪声机制
在应用差分隐私进行隐私保护算法时,目标是输出一个具有差分隐私保障的\(f(D)\),即基于随机算法\(\mathcal{M}(D):=f(D)+\mathbf{z}\),其中\(f(D)\)表示的是查询函数,\(\mathbf{z}\)为随机噪声,\(\mathcal{M}(D)\)表示最后返回的结果,需要处理的数据主要分为两大类,一类是数值型的数据,比如说数据集中病患的数量;另外一类是非数值型的数据,比如喜欢人数最多的颜色。这两者,主体分别是数量(连续数据)和颜色(离散数据)对于数值型的数据,一般采用Laplace或者高斯机制,而对于非数值型的数据,一般采用指数机制并引入一个打分函数,以下对这三种噪声机制进行进一步的介绍:
Laplace机制
记位置参数为0、尺度参数为\(b\)的Laplace分布为\(b\),那么其概率密度函数为\(p(x)=\frac{1}{2 b} \exp \left(-\frac{\mid x \mid}{b}\right)\)。拉普拉斯分布是指数分布的对称版本。
定义6. (Laplace机制) 给定数据集\(D\),设有函数\(f:\mathbb{N}\mid\mathcal{X}\mid \rightarrow \mathbb{R}^{k}\),其敏感度为\(\Delta f\),那么随机算法\(M(D)=f(D)+Y\)提供ε差分隐私保护,其中\(Y\sim \operatorname{Lap}(\Delta f / \varepsilon)\)为随机噪声,服从尺度参数为\(\Delta f / \varepsilon\)的Laplace分布
如下图,从不同参数的Laplace分布可以看出,\(\varepsilon\)越小,引入的噪声越大
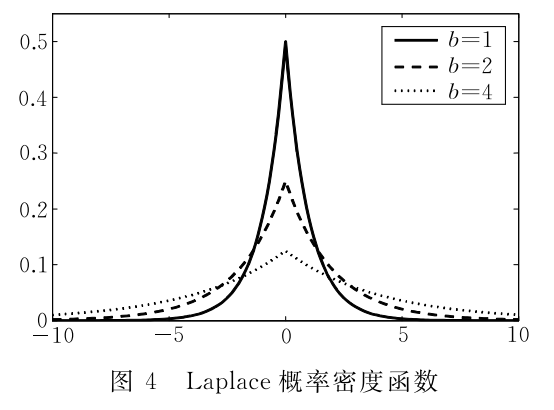
对于一个确定的数据集(即敏感度确定),可以看到,隐私预算越小,噪声越大,结果可用性越小,隐私保护越好。即隐私预算和可用性成正比。
这里的敏感度\(\Delta f\)具体表示为\(\Delta f=\max _{D, D^{\prime}}\mid\mid f(D)-f\left(D^{\prime}\right) \mid\mid_{1}\),即对于相邻数据集\(D\)和\(D'\),一个查询函数\(f(\cdot )\)最大的变化范围,比如查询数量,敏感度就是1。
隐私证明:
\(\begin{aligned}
\frac{p_{x}(z)}{p_{y}(z)} &=\prod_{i=1}^{k}\left(\frac{\exp \left(-\frac{\varepsilon\left|f(x)_{i}-z_{i}\right|}{\Delta f}\right)}{\exp \left(-\frac{\varepsilon\left|f(y)_{i}-z_{i}\right|}{\Delta f}\right)}\right) \\
&=\prod_{i=1}^{k} \exp \left(\frac{\varepsilon\left(\left|f(y)_{i}-z_{i}\right|-\left|f(x)_{i}-z_{i}\right|\right)}{\Delta f}\right) \\
& \leq \prod_{i=1}^{k} \exp \left(\frac{\varepsilon\left|f(x)_{i}-f(y)_{i}\right|}{\Delta f}\right) \\
&=\exp \left(\frac{\varepsilon \cdot\|f(x)-f(y)\|_{1}}{\Delta f}\right) \\
& \leq \exp (\varepsilon),
\end{aligned}\)
这是,代表输出的数据是\(k\)维的,比如查询top-k的数据,是一维的拓展。所以第一个等号表示的是,输出为 \(z\)的概率, \(k\)个输出之间相互独立,都满足拉普拉斯分布,里面将分布概率展开。第二个等号就是简单的化简;第三个不等号是利用绝对值三角不等式;第四个等号利用的是一范数的定义;第五个不等式利用的是上面讲的敏感度的定义。
可用性证明:
假设算法\(f(D)\)计算的是数据集\(D\)的平均值,即\(f(D)=\frac{1}{n} \sum_{X^{(k)} \in D} X^{(k)}\),\(X^{(k)} \in \mathbb{R}^{d}\)
则式子\(\|f(D)-\mathcal{A}(D)\|_{1}=\|\mathbf{z}\|_{1} \leq O\left(\frac{d \Delta f}{\varepsilon n}\right)\)以很高的概率成立
基于其上界表示,可以认为误差与维数\(𝑑\)和敏感度\(\Delta f\)成比例变化
(2)高斯机制
Laplace机制提供的是严格的\(\varepsilon\)-差分隐私机制,而高斯机制则提供的是松弛的 \((\varepsilon,\delta)\)-差分隐私机制。
定义7. (Gaussian mechanisms) 给定数据集\(D\),设有函数\(f:\mathbb{N}\mid\mathcal{X}\mid \rightarrow \mathbb{R}^{k}\),其敏感度为\(\Delta_2 f\),对于任意\(\delta \in(0,1)\),随机算法\(M(D)=f(D)+Y\)提供 (𝜀, 𝛿)差分隐私保护,其中\(Y \sim N\left(0, \sigma^{2}\right)\)为随机噪声,满足\(\sigma>\frac{\sqrt{2 \ln (1.25 / \delta)} \Delta_2 f}{\varepsilon}\)
这里的敏感度\(\Delta_2 f\)具体表示为\(\Delta_2 f=\max _{D, D^{\prime}}\mid\mid f(D)-f\left(D^{\prime}\right) \mid\mid_{2}\),刚才Laplace定义的是 \(L_1\),这里的高斯定义的是 \(L_2\)。
高斯分布的标准差\(\sigma\) 决定了噪声的尺度了;\(\varepsilon\)表示隐私预算,和噪声成负相关;\(\delta\)表示松弛项,比如设置为\(10^{-5}\) ,就表示只能容忍\(10^{-5}\)的概率违反严格差分隐私。高斯机制无法保证任何有限𝜀的𝜀-DP。
(3)指数机制——应对离散查询问题
Laplace机制与高斯机制所应对的都是数值查询问题,诸如”张三患病的概率是多少,A公司员工的平均工资是多少”,这些问题的查询都可以简单地对输出的数值结果加入噪声实现差分隐私。而对于非数值型查询问题,诸如”这个公司中职员占比最多的族裔是哪个,A商品能够达到最大利润的定价是多少”这一类查询问题而言,它的输出范围往往是某个离散数据集合\(\mathcal{R}=\left\{R_{1}, R_{2}, \ldots, R_{N}\right\}\),而不是连续数据。例如,\(\mathcal{R}=\{\text{White},\text{Yellow},\text{Black}\}\),或是\(R=\{\$4.02,\$1.02,\$0.98\}\)(注意因为消费者的分层,最高利润的定价往往不是一个连续分布,而是离散取值)。对于这种问题,往往采用指数机制,为每一个可能的回答分配对应的概率,例如对每一个\(r\in\mathcal{R}\)分配价值得分函数\(q(D,r)\),那么满足\(\epsilon-\)差分隐私的查询分布可以采用指数族进行: \(\forall r \in \mathcal{R}, \Pr[r]\sim\exp(\frac{\epsilon\cdot q(D,r)}{2\Delta})\)
性质
post-processing
考虑这样一种场景,如果攻击者非常认真地考虑差分隐私计算的输出,例如将其输入设计的神经网络来破坏隐私,那会导致怎样的后果?其实不需要担心,差分隐私仍然能够由后处理(post-processing)性质得到保障,这意味着在差分隐私机制输出之上运行任意计算不会减少相应的\(\varepsilon\)保障。
这不仅可以防止聪明的对手,还为我们设计差分隐私机制提供了很大的灵活性:一旦在数据处理pipeline的任何地方执行差分隐私,无论算法后续对该结果进行任何处理,均不会影响其隐私保护的效果。
因而,在分布式机器学习算法中,我们可以将噪声加在原始数据,梯度(gradient),本地模型(local model)等等,只需在其中某处保证了差分隐私即可保证算法在本地的隐私保护效果。

Composition
差分隐私的Composition机制是将多个差分隐私算法结合在一起并且仍然保证满足差分隐私,是差分隐私算法落地的关键。composition theorem所研究的问题为:已知一个随机函数的隐私损失,那么\(k\)个随机函数总的隐私损失是多少呢?在每一个随机函数所加的噪声(noise)相互独立时,隐私损失是可以累加的。这意味着如果某个机制保证单个查询具有 ε=1,若想要发出三个查询,则花费的总隐私预算将为 ε=3。形式上,差分隐私的顺序组合定理表示为:
定义8. (Basic composition theorem) 设\(\mathcal{A}_{1:k}\)是\(k\)个具有独立噪声的机制,令\(\mathcal{A}_{i}\)满足\(\left ( \varepsilon_i,\delta_i \right ) -DP\)。那么\(\mathcal{A}_{1:k}\)的自适应组合满足\(\left(\sum_{i} \varepsilon_{i}, \sum_{i} \delta_{i}\right)-\mathrm{DP}\)。
隐私损失是一个随机变量,注意到随机变量除了本身的值有一个范围,他的期望也有一个范围。基本的组成定理没有利用所添加噪声的独立性,是一个松散的界限。而求多个随机变量累加的和,不应该仅仅将其上界进行累加,应该同时考虑其本身值和期望的范围,从而得到一个更紧的上界。基于这一点提出了高级的组成定理,以下为高级组成定理的定义:
定义9. ( Advanced composition theorem) 设\(\mathcal{A}_{1:k}\)是\(k\)个具有独立噪声的机制,令\(\mathcal{A}_{i}\)满足\(\left ( \varepsilon,\delta \right ) -DP\)。那么对于小的\(\varepsilon\)值\(\mathcal{A}_{1:k}\)的自适应组合满足\((O(\sqrt{k} \varepsilon), O(k \delta))-\mathrm{DP}\)。
Rényi差分隐私
上文讨论了三个传统的差分隐私机制:指数机制,Laplace机制以及Gaussian机制。其中,指数机制应对离散查询,Laplace机制提供了严格的\(\left ( \varepsilon,0 \right )-\)DP,而Gaussian机制通过正态分布噪声将差分隐私松弛到带有余项\(\delta\)的\(\left ( \varepsilon,\delta \right )-\)DP。但是,这些机制还存在一些缺点:首先,传统的差分隐私机制需要对所有的相邻数据库\(D,D'\in \mathbb{N}^{\vert \mathcal{X}\vert}\)在所有的随机\(\mathcal{S}\subset \mathcal{O}\)上计算
此外,对于一个确定的正态噪声\(N(0,\sigma^2)\),可以找到无数对符合要求的\((\epsilon,\delta)\),而它们大概是互为倒数的关系(\(\sqrt{\delta}\epsilon\propto \frac{1}{\delta}\)),如何选取最合适的\((\epsilon,\delta)\)对是一个值得研究的问题。最后,Composition定理对于\((\epsilon,\delta)\)都要求线性相加,这样的隐私界对于大部分机器学习模型而言都过于宽松了。因此,Google Brain的Ilya Mironov在2017年提出了Rényi差分隐私(RDP)。相比于传统的\(\left ( \varepsilon,\delta \right )-\)DP, Rényi-DP 具有两个优势:首先,RDP给出了\(\left ( \varepsilon,\delta \right )\)间更为准确的关系,能够允许我们有效选择合适的差分隐私界。其次,RDP的Composition定理所给出的累计隐私损失更小,因此在相同的隐私界下能够得到更高的模型准确性,注入更小的噪声。 Rényi-DP 基于 Rényi散度提出,我们首先对 Rényi散度进行介绍。
定义
定义10. (Rényi 散度)给定两个满足离散分布的随机变量\(\mathbf{X}\)和\(\mathbf{Y}\),它们具有 \(n\) 个可能的值,每个值分别具有正概率 \(p_i\) 和\(q_i\),\(\mathbf{X}\)和\(\mathbf{Y}\)的 Rényi 散度定义为 \(D_{\alpha}(\mathbf{X}\Vert \mathbf{Y})=\frac{1}{\alpha-1} \log \left(\sum_{i=1}^{n} \frac{p_{i}^{\alpha}}{q_{i}^{\alpha-1}}\right)\) 其中\(\alpha > 0\)并且\(\alpha \neq 1\)。对于Rényi散度已经有很多研究,推荐阅读Rényi散度与KL散度的关系。Rényi散度有如下几个性质:
-
对于两个正态分布\(\mathbf{X}\sim N(\mu_0,\sigma_0^2),\mathbf{Y}\sim N(\mu_1,\sigma_1^2)\),\(D_{\alpha}(\mathbf{X}\Vert \mathbf{Y})=\frac{\alpha\Vert\mu_0-\mu_1\Vert_2^2}{2[(1-\alpha)\sigma_0^2+\alpha\sigma_1^2]}+\frac{1}{1-\alpha}\ln\frac{(1-\alpha)\sigma_0^2+\alpha\sigma_1^2}{\sigma_0^{1-\alpha}\sigma_1^\alpha}\)
-
\(D_{\alpha}(\mathbf{X}\Vert \mathbf{Y})\)关于\(\alpha\)是单调不减函数
-
定义\(D_{0}(\mathbf{X}\Vert \mathbf{Y})=\lim_{\alpha\rightarrow 0,\alpha>0}D_{\alpha}(\mathbf{X}\Vert \mathbf{Y})\),则\(D_{0}(\mathbf{X}\Vert \mathbf{Y})=-\ln(\sum_{i:p_i>0}q_i)\)。
-
定义\(D_{1}(\mathbf{X}\Vert \mathbf{Y})=\lim_{\alpha\rightarrow 1}D_{\alpha}(\mathbf{X}\Vert \mathbf{Y})\),则\(D_{1}(\mathbf{X}\Vert \mathbf{Y})=D_{KL}(\mathbf{X}\Vert \mathbf{Y})\)。
注意这条性质的证明实际上有点复杂,需要先用\(\ln_{x\rightarrow 1} x=x-1\),注意到\(\log \left(\sum_{i=1}^{n} \frac{p_{i}^{\alpha}}{q_{i}^{\alpha-1}}\right)\rightarrow^{\alpha\rightarrow1}1\),因此\(\log \left(\sum_{i=1}^{n} \frac{p_{i}^{\alpha}}{q_{i}^{\alpha-1}}\right)\rightarrow \sum_{i=1}^{n} \frac{p_{i}^{\alpha}}{q_{i}^{\alpha-1}}-1\),然后将原式写成 \(\lim_{\alpha\rightarrow 1}D_{\alpha}(\mathbf{X}\Vert \mathbf{Y})=\frac{1}{\alpha-1} \left(\sum_{i=1}^{n} \frac{p_{i}^{\alpha}}{q_{i}^{\alpha-1}}-1\right)=\sum_{p_i,q_i>0}\lim_{\alpha\rightarrow 1}\frac{p_i-p_{i}^{\alpha}q_{i}^{1-\alpha}}{1-\alpha}\) 再利用积分中值定理 \(\forall p,q>0,\frac{p-p^\alpha q^{1-\alpha}}{1-\alpha}=\frac{1}{1-\alpha}\int_{\alpha}^1p^zq^{1-z}\ln \frac{p}{q}dz=p^{\sigma}q^{1-\sigma}\ln \frac{p}{q},\sigma \in (\alpha,1)\) 代入后就是\(\lim_{\alpha\rightarrow 1}D_{\alpha}(\mathbf{X}\Vert \mathbf{Y})=\sum p_i \ln\frac{p_i}{q_i}=D_{KL}(\mathbf{X}\Vert \mathbf{Y})\)。
-
定义\(D_{\infty}(\mathbf{X}\Vert \mathbf{Y})=\lim_{\alpha\rightarrow \infty}D_{\alpha}(\mathbf{X}\Vert \mathbf{Y})\),则\(D_{\infty}(\mathbf{X}\Vert \mathbf{Y})=\ln \sup_{\mathcal{S}\subset \mathcal{O}}\frac{\operatorname{Pr}[\mathbf{X} \in S]}{\operatorname{Pr}\left[\mathbf{Y} \in S\right]}\)。
利用Rényi 散度,我们可以如下定义Rényi differential privacy:
定义11. (Rényi differential privacy) 我们称\(\mathbb{N}^{\vert \mathcal{X}\vert}\)上的随机算法\(\mathcal{M}\)满足\(\left ( \alpha ,\epsilon \right )\)-Rényi differentially private,如果对于对于所有的相邻数据库\(D,D'\in \mathbb{N}^{\vert \mathcal{X}\vert}\),满足 \(D_{\alpha}\left(\mathcal{M}(D) \| \mathcal{M}\left(D^{\prime}\right)\right) \leq \epsilon\)
(RDP与DP的关系) 注意到性质2中\(D_{\alpha}(\mathbf{X}\Vert \mathbf{Y})\)关于\(\alpha\)是单调不减函数,利用Rényi散度的性质五,我们注意到\((\epsilon,0)-\)DP等价于满足\((\infty,\epsilon)-\)RDP。这也能看出RDP和DP具有类似于上界的关系,相比于DP需要遍历所有可能的事件\(\mathcal{S}\subset \mathcal{O}\),RDP只需要计算一次距离散度,大大减少了计算负担。此外,我们不加证明地给出以下结论:如果\(f\)满足\((\alpha,\epsilon)-\)RDP,那么\(\forall \delta \in (0,1)\),它也同样满足\((\epsilon+\frac{\log\delta}{1-\alpha},\delta)\)-DP。比起传统的差分隐私,利用RDP所得的\((\epsilon+\frac{\log\delta}{1-\alpha},\delta)\)-DP把\((\epsilon,\delta)\)两项联系在了一起,使得我们可以通过调控\(\delta\)将指数项的压力放在后面的常数项,从而得到最好的差分隐私方案。
(定义12. Gaussian mechanisms for Rényi differential privacy) 与DP类似,指数机制,Lapace机制以及高斯机制同样适用于RDP。以高斯机制为例,给定数据集\(D\),设有函数\(f:\mathbb{N}\mid\mathcal{X}\mid \rightarrow \mathbb{R}^{k}\),其敏感度\(\Delta_2 f=1\),则添加随机噪声\(Y \sim N\left(0, \sigma^{2}\right)\)的随机算法\(M(D)=f(D)+Y\)满足\((\alpha,\alpha/2\sigma^2)-\)RDP。
RDP的Composition定理
与DP类似,RDP满足如下的Composition定理:
定义12. (Rényi composition theorem) 令\(f:D\rightarrow R_1\)满足\((\alpha,\epsilon_1)-\)RDP,\(g:D\times R_1\rightarrow R_2\)满足\((\alpha,\epsilon_2)-\)RDP,那么由\((\mathbf{X},\mathbf{Y}),\mathbf{X}\sim f(D),\mathbf{Y}\sim g(\mathbf{X},D)\)所组合的机制满足\((\alpha,\epsilon_1+\epsilon_2)-\)RDP。
此外,将\((\epsilon,0)-\)DP看作是RDP的一个上界(即\(\alpha\rightarrow \infty\),那么在\((\epsilon,0)-\)DP上所得的传统结论一般也可以推广到RDP上,如下引理所述:

利用这个定理,对于复合机制,我们可以用RDP给出更小的隐私损失:由\(k\)个机制进行composition所得的系统,其中每一个机制都添加分布为\(N(0,\sigma^2)\)的噪声(即满足\((\alpha,\alpha/2\sigma^2)-\)RDP,\((\alpha/2\sigma^2+\frac{\log\delta}{1-\alpha},\delta)\)-DP),那么整个复合系统就相当于添加分布为\(N(0,\sigma^2/k)\)的噪声,满足\((\alpha,k\alpha/2\sigma^2)-\)RDP,即\((n\alpha/2\sigma^2+\frac{\log\delta}{1-\alpha},\delta)\)-DP。注意到这里的优势是仅仅在指数项增加了\(k\)倍,没有影响常数项,所以其隐私损失更小了。
RDP的总结与比较优势
- RDP是DP的一种自然的推广,当\(\alpha\rightarrow \infty\),RDP等价于DP。而\(D_{\alpha}(\mathbf{X}\Vert \mathbf{Y})\)关于\(\alpha\)是单调不减函数,所以DP是RDP的一个上界,RDP的Bound更紧。
- RDP与DP共享了很多特性,而RDP的计算更加简单,将复杂的遍历计算归结于一个散度计算,这使得RDP可以在实际中使用。
- RDP在高斯机制下的计算很简单,结论更加有用。
- 在相同的隐私损失下,RDP能够添加更小的噪声,使得查询更加准确。
满足隐私的机器学习
在上文中,我们对隐私进行了定性的定义。在应用过程中,隐私保护的目的则有更简单具体描述:对于任何数据分析员,要求分析员在对数据库进行分析后,对数据库中每一个个体的了解不会超过其在分析开始之前的了解。那么,为了达成这种目的,我们需要对差分隐私提出两个疑问:对于一个数据分析过程,应当在什么时机,以什么方式引入并实现隐私保护机制呢?
在第一节对于侵犯隐私行为的讨论中,我们知道引入实时的监督者并不能保障个人隐私安全,因此差分隐私的引入时机必然是在数据库发布后,到所有的数据分析工作开始之前。因此,我们沿用[2]中的描述,对差分隐私所扮演的角色进行描述:差分隐私相当于一个值得信赖的数据库管理员,它的目的是保护数据库中每一行记录,同时允许整个数据库能够被分析。这个管理员在数据库面向分析员发布前,对原始数据库进行一些操作:对数据库进行合成(例如,依据原始数据产生同分布的虚拟数据)、对某些统计结果进行汇总,或者自行清除数据库某些离群数据,然后发布新的数据库,销毁原始数据库。此后,差分隐私不再发挥作用,对于新的数据库,允许数据分析员进行自适应的查询,包括根据当前的查询结果,以及分析员的先验知识,自行决定下一次查询。差分隐私希望经过这种操作后,对于任何可能的查询,以及对查询结果的一系列加工都不会泄露个体隐私。
机密计算可以做到在训练过程中保护数据的隐私。那么训练后的模型会造成隐私训练数据的泄露吗?答案是可能的,因为机器学习的模型都会在一定程度上过拟合,模型自身会记住(部分)训练数据,从而导致发布模型会造成隐私训练数据的泄露。差分隐私(Differential Privacy, DP) 可以衡量和控制模型对训练数据的泄露。这一部分将介绍具有隐私保障的机器学习范式,以及一种基于差分隐私理论的随机梯度下降算法(DP-SGD)
具有隐私保障的机器学习
机器学习的一般流程为:设计目标函数即经验风险最小化(Empirical Risk Minimization, ERM),训练过程一般是基于梯度的优化算法,最后输出训练好的模型。对应地,根据加噪声的时机,差分隐私机器学习有三种实现方法——目标扰动(Objective Perturbation),即在目标函数上添加噪声;梯度扰动(Gradient Perturbation, GP),即在梯度上添噪声;输出扰动(Output Perturbation),即在最后输出上添加噪声。若添加的噪声很大,会带来模型的性能损失,但太小又不能很好地保护隐私。因此,差分隐私机器学习就是研究如何在给定的隐私损失的限制下,添加最少的噪声并取得最好的性能。
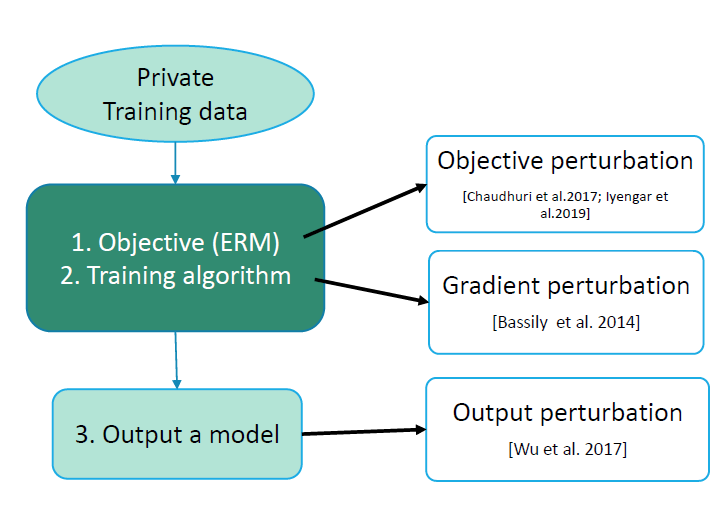
对于机制\(\mathcal{M}\),一种可能性是仅考虑模型输出的隐私。 这确实是一个隐私预测的有效选项,但它具有许多附加条件:模型仍然可以记忆,因此需要由推理系统来安全地执行这些约束。 此外,这会阻止我们发布ML 模型,因为如果有人看到权重,隐私保证将丢失。 这意味着在移动设备上部署的安全性将大大降低。
出于这个原因,如果我们可以在模型训练期间加入 DP 机制,这样生成的模型可以安全地发布,这是一种较为合理的方案。 接下来将介绍在模型训练期间,对梯度加入噪声后再进行更新的 DP-SGD 算法。
DP-SGD
深度学习最常用的优化算法时随机梯度下降算法(SGD),这里介绍的就是为其提供差分隐私保证的DP-SGD算法,如下所示的SGD和DP-SGD的简化版的代码流程,可以观察到DP-SGD就是在原始的SGD算法上对梯度增加了随机生成的噪声,并用这个带有噪声的梯度对参数进行更新。

论文中关于DP-SGD的其他细节:
-
噪声的大小取决于梯度的敏感度\(\max _{D, D^{\prime}} \max _{\theta}\left\|\nabla L(\theta ; D)-\nabla L\left(\theta ; D^{\prime}\right)\right\|\);敏感度取决于损失的平滑性,也就是当损失越平滑加入的噪声越少;
-
还可以将单个梯度裁剪到一个预定义的阈值,论文中DP-SGD的完整代码如下,由于差分隐私保护要求限制每个样本对于最终梯度$\tilde{g} _t$的影响,鉴于梯度的取值范围无先验限定,故采用\(L_2\)范数。首先对每个梯度进行裁剪,即梯度向量 $g $由 $g/\max (1,\left | g \right |_2/C )$替换,其中 $\mathcal{C} $为剪切阈值。裁剪后结果为:若$\left | g \right |_2\le C$,则保留 \(g_t\),若$\left | g \right |_2> C$, 则将其缩小为常量$ \mathcal{C} $。

(1)DP-SGD的隐私证明
对于DP-SGD的隐私证明是直接基于Renyi差分隐私给定的敏感度\(𝑆\)。
每次调用满足\(\left ( \alpha,\gamma (\alpha ) \right )-RDP\)的高斯机制,其中\(\gamma (\alpha )=\frac{S\alpha }{\sigma^2 }\),基于RDP的组成定理,经过\(T\)次的迭代满足\(( \alpha,T\gamma (\alpha ) )-RDP\)
将\(( \alpha,T\gamma (\alpha ) )-RDP\)转换为\(\left ( \varepsilon,\delta \right ) -DP\),然后 \(\alpha \in \left ( 0,\infty \right )\)的范围内优化\(\left ( \varepsilon,\delta \right )\)
对于DP-SGD,我们需要考虑通过子抽样来进行的隐私加强
(2)DP-SGD的可用性证明
从高斯分布中提取的梯度扰动,即往梯度中加入噪声,可以通过噪声梯度下降来分析 DP-SGD 或 DP-GD 的效用,其中噪声取决于 \(\left ( \varepsilon,\delta \right )\)和迭代次数;
DP-SGD的一个主要问题是噪声大小的选取,DP-SGD 的误差依赖于维度\(p\),也就是模型中的参数数量。 [Bassily et al. 2014]中证明DP-SGD的误差上界为\(O\left(\frac{\sqrt{p}}{n \varepsilon}\right)\),在最坏的情况下,这种对 \(p\) 的依赖是不可避免的,效用随着模型的维度变大而极速下降,这点在经验上得到了证明,相关细节可以参考论文。 [Tramer&Boneh 2021]。
然而,现在许多现代机器学习任务都涉及训练非常大的模型,其参数数量远大于训练样本数量。对于这些大型模型,对\(p\) 的误差依赖性可能是对于具有隐私保障的ERM 的障碍。
(3)DP-SGD的实验表现
以下是DP-SGD的一些实验结果,实验在不同的数据集和\(\varepsilon\)值所对应的隐私保护水平下进行,代码基于[Opacus,BackPACK]实现,DP-SGD降低了计算各个梯度的成本[Abadi et al. 2016, Code in PyTorch]
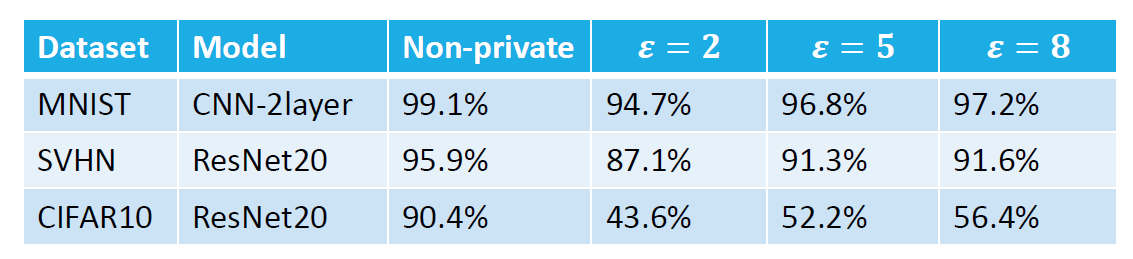
让我们具体代入数值从而得到一些直观的感受,当\(\varepsilon=8\),基于最核心的差分隐私公式\(\frac{\operatorname{Pr}[\mathcal{M}(D) \in S]}{\operatorname{Pr}\left[\mathcal{M}\left(D^{\prime}\right) \in S\right]} \leq e^{\varepsilon}\)可以得出\(e^8\approx2981\),这对于两个概率分布是一个非常宽松的界,可以说在这种情况下提供的隐私保护水平有限。
DP-SGD的保障和不足
如何通过实验去衡量DP-SGD的隐私保障呢?根据定义,差分隐私为数据注毒攻击提供了一个可证明的防御,也就是基于差分隐私的随机算法,可以确定对手成功预测的概率上限,从而量化隐私信息的最大泄漏程度。
关于DP隐私性能的验证数据泄漏形式化,其中对手必须预测模型是在数据集\(D\)上训练的,还是在其邻近数据集\(D'\)上训练的。如果训练算法没有明显地增加对手成功猜测模型在哪个数据集上训练的几率,那么该算法具有差分隐私保障。因此,隐私分析的目的是限制任何对手能够成功猜测模型训练的数据集的概率上限,可以通过设计较强的数据注毒攻击来衡量差分隐私算法提供的隐私的下限。
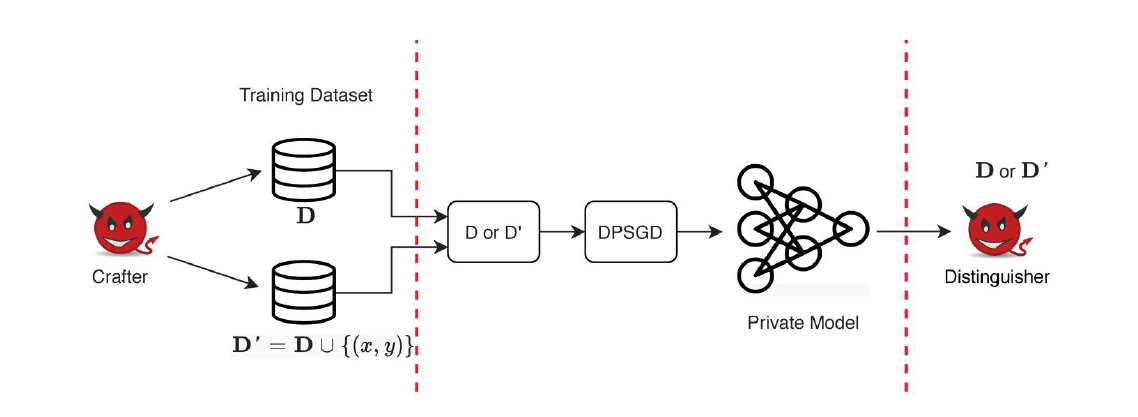
具体的攻击过程如下图所示,第一个算法,crafter构建了一对邻近数据集\(D\)和\(D'\)。然后,crafter在这两个数据集上采用差分隐私算法(比如DP-SGD)分别训练模型。第二个算法,distinguisher的任务是输入邻近数据集\(D\)和\(D'\),以及训练好的模型的输出,判断使用了哪个数据集。
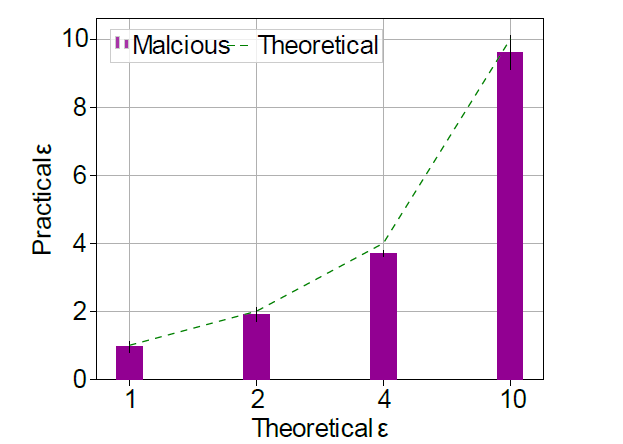
如下图实验结果所示,绿色虚线对应于理论上可证明的上限,每个紫色条形为对应不同隐私保障水平\(\varepsilon\) ,差分隐私模型应对数据集攻击所提供的隐私的下界,可以看出DP所保障的与经验下界相匹配
以下为强度从弱到强的六种攻击模型类型
- API access:数据所有者将收集数据并自行训练模型,对手无法控制和修改训练程序或数据集。对手只能通过黑匣子访问经过训练的模型。
- Static Poison Attack:实例化我们的对手来构造最坏情况下的恶意输入,即在一个数据集上训练一个模型时,只包含一种类型的个体(年龄、性别、种族等),并往代表性不足的群体中插入一个训练样本,看是否会增加模型中泄露隐私信息的可能性。对手可以访问最终经过训练的模型。
- Intermediate Poison Attack:假设对手可以访问所有中间模型参数,并公开所有中间模型。这使我们能够研究这一额外能力的相对重要性。
- Adaptive Poison Attack:不要求插入的样本在 epoch 之间保持不变:在每次迭代的 epoch里,重新实例化最坏情况的插入样本。 这能够去评估mini-batch方式是否会影响能够提供的下限。
- Gradient Attack:随着联邦学习继续受到越来越多的关注,估计在这种环境中训练模型会导致多少额外的隐私泄漏也很重要。 在联邦学习中,恶意实体可以对梯度本身进行注毒攻击。因此,该对手能够直接修改梯度。
- Dataset Attack:最后也是最强大的攻击,可以利用所有对手的能力。评估此种攻击能够证明 DP-SGD的分析是严格的。
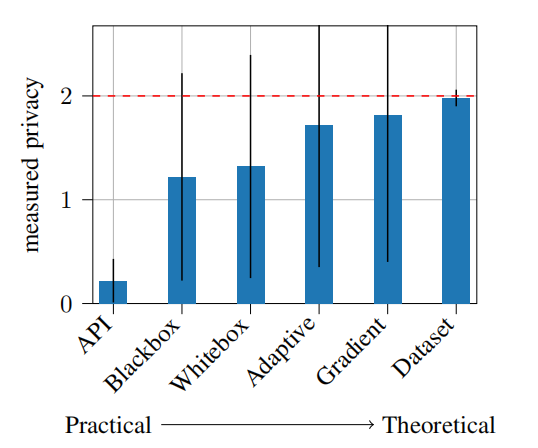
如下图结果显示,绘制了在 MNIST 上训练具有 ε = 2 差分隐私的模型时测量的 ε。 红色虚线对应于可证明的上限,每个条形为应对逐渐强大的对手所提供的隐私。 在最现实的环境中(API),隐私训练提供了更多经验上的隐私;当我们完整的攻击能力时,也就是当可以对数据集进行访问的时候(Dataset Attack),提供的隐私下限表明 DP-SGD 上限很紧。
DP-SGD的不足之处
- 不足1:效用取决于输出维度,对于大型模型,效用下降较大。
- 不足2:计算开销,与SGD相比,处理每个样本的梯度需要更多的计算和更多的内存
提升隐私机器学习的方法
隐藏中间更新
DP-SGD公开迭代过程中所有的参数\((\theta_1,...,\theta_T)\),每一步都有DP保障,通过组合定理累计获得总的隐私,但是我们往往只需要最终的那个模型参数输出\(\theta_T\),直观上,\(\theta_T\)会比\((\theta_1,...,\theta_T)\)所需的隐私预算小,但我们该如何从理论上去证明这一点呢?
-
Rishav et al. [2021] 我们证明,对于平滑且强凸的损失函数,隐私损失呈指数级快速收敛,这是对组合定理的重大改进。
\[\varepsilon=O\left(1-\exp \left(-\frac{O(T)}{2}\right)\right)\] -
Feldman et al. [2018] 证明对于收缩迭代,不发布中间结果会极大程度上加强隐私保证
Open questions:如何论证隐藏通用迭代算法的中间更新的好处?
利用学习问题的先验
先验知识是指除训练数据外所有关于问题的可用信息,利用学习问题的先验,比如一般来说包含差分隐私的算法如DP-SGD有严重的模型维度依赖,也就是更大的模型导致更大的噪声,导致更低的可用性,但是如果我们能够利用学习问题的稀疏结构 [Kalwar et al.2015, Cai et al. 2020]那么就可以只需要去依赖稀疏后的维度,而不必要去依赖模型的完全维度,从而降低噪声提高可用性。对于一般的学习场景,比如在CIFAR10上训练ResNet这种完全不稀疏的网络结构,该如何去利用学习问题的先验?tutorial列出了以下几种可能性,更具体的细节可以参考相关的论文
- 通过知识迁移 [Papernot et al.2017, Papernot et al.2018]
- 通过一般的结构 [Tople et al.2020]
- 通过样本间梯度的冗余 [Zhou et al.2021, Yu et al.2021a]
- 通过一个先验对角缩放矩阵 [Asi et al.2021]
- 通过NN层梯度的低秩 [Yu et al.2021b]
(1)通过知识迁移
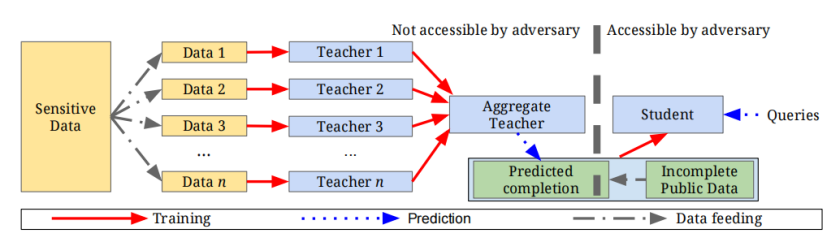
PATE(Private Aggregation of Teacher Ensembles)为教师集成的隐私聚合模型,为Papernot等人提出的一种机器学习框架。该框架允许使用隐私的数据进行半监督学习,同时保留直观和强大的隐私保证。
PATE基于以下思想:如果对不相交数据训练的多个模型在输入上达成共识,则不会泄漏有关其训练样本的隐私数据,因为所有模型均得出相同的结论。仅通过查询在不同“教师”模型之间具有高度相关性的输出,提供了直观的隐私。另一方面,如果未达成共识,则检索随机的输出可提供强大的隐私保证。该随机选择可以通过和噪声的聚合来获得,因此可以通过该方法实现\(\left ( \varepsilon,\delta \right )\)差分隐私。
此外,PATE框架还包含一个额外的步骤,添加了一个“学生”模型,该模型从教师标记的公共数据中学习,这样做消除了在后续查询中的需要查询访问教师。确保了无法对教师的隐私数据进行任何攻击,无论是通过多次查询还是通过模型的参数检查,确保了学生模型仅学习教师提供的共识知识。
(2)利用样本间梯度的冗余
DP-SGD的主要缺点在于有较为严重的维度依赖,也就是更大的模型导致更大的噪声,导致更低的可用性,Projected DP-SGD该方法的主要思想来源是在深度网络的训练中随机梯度停留在低维空间中。直觉上,梯度下降所需的大部分信息都embedding在随机梯度的顶部特征空间中。
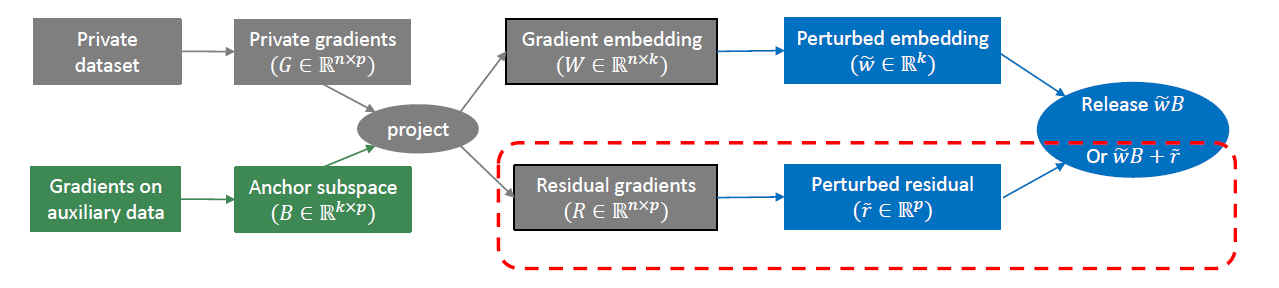
就像上面介绍的那样,维数依赖性是应用差分隐私(DP)的一个本质困难。为了解决“维数”挑战,提出了一种算法“梯度嵌入扰动(Gradient embedding perturbation, GEP)”。其基本想法是模型维数虽然很大,但梯度却通常在一个低维空间中,这不仅符合人们对数据生长在低维流形上的认知,也在实践中可以被广泛验证。利用这个性质,可以将把模型梯度先投影到一个低维空间后再做扰动,从而巧妙地绕开了维数依赖。
具体来说如下图所示,在每个梯度下降步骤中,首先用辅助数据估计一个锚子空间,然后将private梯度投影到子空间,得到一个低维梯度embedding和一个小范数的残差梯度,之后在保证差分隐私预算的前提下,分别扰动梯度embedding和残差梯度。总的来说,可以使用比原来的梯度扰动低得多的扰动,以保证相同的隐私保障水平。
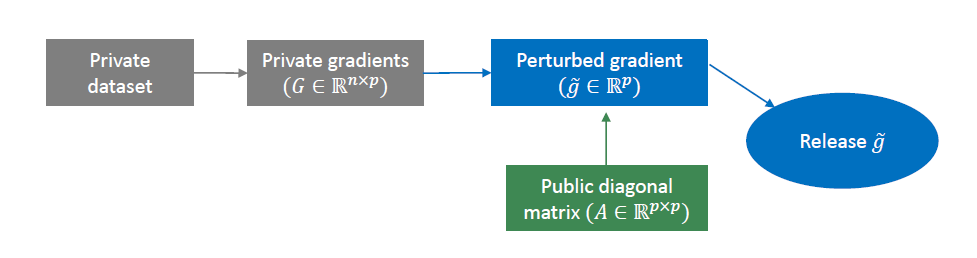
(3)利用先验对角缩放矩阵
这个方法同样是针对DP-SGD的较为严重的维度依赖的缺点,核心步骤是用先验知识给出的对角矩阵缩放噪声,因此同样可以达到使用比原来的梯度扰动低得多的扰动,以保证相同的隐私保障水平的目的。具体算法细节参考论文
(4)通过NN层梯度的低秩
RGP: Reparametrized gradient perturbation,利用权重矩阵的低秩属性
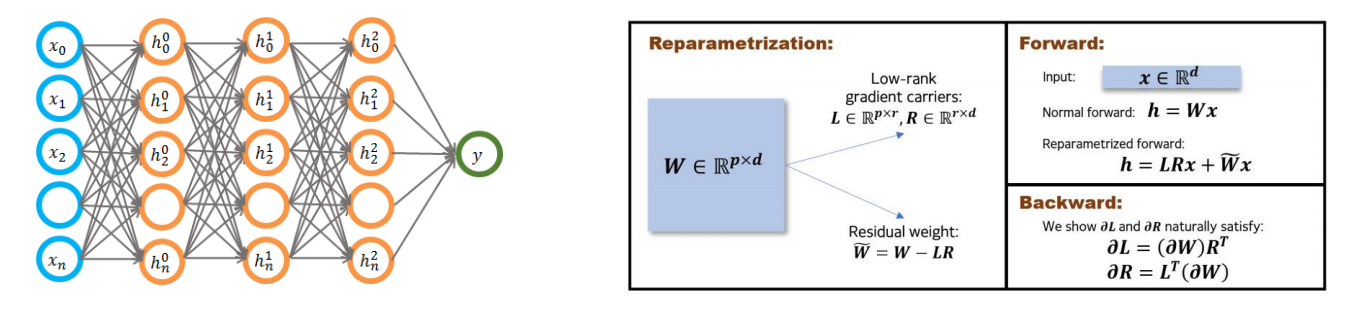
这个方法是一种新的参数化方案,主要是针对在大型神经网络上应用DP-SGD的以下两个挑战,即存储单个梯度的巨大内存开销,以及具有维度依赖的加噪方式。该方法的名称叫做重新参数化梯度扰动(RGP,Reparametrized gradient perturbation),具体来说,就是使用两个小维度的gradient-carrier 矩阵\(L,R\)和一个residual weight矩阵\(\tilde{W}\)对每个权重矩阵\(W\)进行重新参数化。这种重新参数化的方式保持前向/后向传播的过程不变,同时只计算投影梯度而不计算梯度本身,扰动gradient-carrier矩阵上的梯度,并从噪声梯度重建原始权重的更新。
用差分隐私技术改进机器学习算法
在上文中,我们介绍了差分隐私框架下的隐私保护基本概念,以及满足差分隐私要求的机器学习训练方法。通过在训练过程中控制梯度的范围,并对参数梯度添加噪声,可以令训练出的机器学习模型满足\((\epsilon,\delta)-\)DP,从而抵御差分攻击。在机器学习的研究中,加噪本身可以看作是一种正则化方法,那么差分隐私技术本身是否可以看作是一种正则器呢?它是否可以帮助提高机器学习算法的性能呢?本章节主要介绍用差分隐私技术改进机器学习的一些方法,分为理论和经验两方面:理论上,差分隐私可以用于分析机器学习模型的泛化能力、算法的稳定性以及机器学习的核心原理;经验上,差分隐私也可以用于抵御其他对机器学习模型的攻击。
通过差分隐私改进机器学习的PAC泛化界
机器学习模型往往由两步进行训练:首先,从某个未知的数据分布\(\mathcal{D}\)中采样m个样本,记为\(S=(\mathbf{z_1},\mathbf{z_2},\cdots, \mathbf{z_m})\),然后确定一个参数为\(\mathbf{w}\in \mathbb{R}^p\)的分类器,利用损失函数\(\frac{1}{m}\sum_{i=1}^{m}l(\mathbf{w},\mathbf{z}_i)\)训练模型。我们将给定一组采样\(S\)以及对应的损失函数后,训练所得的的所有分类器的参数分布记为\(Q\)(注意到因为参数初始化是随机初始化,因此我们会得到多个参数不完全一致的分类器,它们构成了分布\(Q\)),而此时我们利用样本集\(S\)进行模型预测的整体损失为 \(L_S(Q)=\frac{1}{m}\sum_{i=1}^{m}\mathbb{E}_{\mathbf{w}\sim Q}[l(\mathbf{w},\mathbf{z}_i)]\) 注意到\(S\)是样本集,而我们希望模型泛化到真实的分布\(\mathcal{D}\),在真实分布上的损失为 \(L_{\mathcal{D}}(Q)=\sum_{\mathbf{z}\sim \mathcal{D}}\mathbb{E}_{\mathbf{w}\sim Q}[l(\mathbf{w},\mathbf{z})]\) 记它们之间的差异为\(\Delta(L_S(Q),L_{\mathcal{D}}(Q))\),PAC泛化界主要研究从采样集\(S\)泛化到真实分布\(\mathcal{D}\)的泛化误差,而差分隐私对该误差界提出了新的改进。假设我们所希望模型学习的参数分布\(P(S)\)满足\(\epsilon-\)DP,文章Data-dependent PAC-Bayes priors via differential privacy指出,基于差分隐私的下述PAC界以\(1-\delta\)的概率成立:

运用DP 抵抗对深度神经网络的攻击
成员推理攻击是对神经网络隐私泄露的主要攻击手段。由于神经网络的训练过程中会对训练集进行一定程度的过拟合,因此模型对于训练集中的数据预测会更加准确,也更加有信心。基于这一特性,成员推理攻击 [Yu et al. 2021]就是通过模型预测来判断某数据是否是某个机器学习模型训练集的成员,如下图所示:
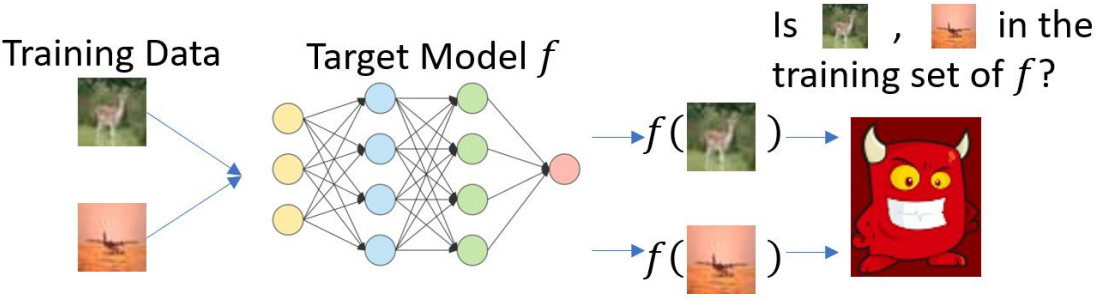
差分隐私可以抵御成员推理攻击。实验结果[Bernau et al., 2019]显示 ,在没有经过差分隐私训练的情况下,成员推理攻击能够以大于50%的概率成功。而在\(\varepsilon=8\)的差分隐私要求下,能够使得成员推理准确率下降到50%,即使得成员推理攻击失效。因此,使用差分隐私训练的模型对成员推理攻击具有鲁棒性。

此外,还有大量研究探索了差分隐私训练对其它攻击的影响。现有工作指出,满足\((\epsilon,\delta)-\)DP的模型对以下攻击具有鲁棒性:
- 数据注毒攻击 [Ma et al. 2019, Hong et al. 2020]
- 梯度匹配攻击(即通过梯度还原输入图像,也称重建攻击) [Zhu et al. 2019]
- 对抗样本攻击 [Lecuyer et al. 2019]
- 模型逆向攻击(通过模型参数还原输入图像的逆向攻击,如仅知道一个人的姓名,通过人脸识别系统给出的置信度还原人脸) [Carlini et al. 2019]
进一步的工作
该部分将概述接下来和隐私保护相关的研究方向的可能性,包括基于差分隐私与差分隐私之外的方向,列出相关论文的链接,具体细节可参考对应论文
基于差分隐私
-
在性能效率:无隐私保障的学习算法与隐私保障的学习算法之间存在较大的性能差距,同时对于训练一个非常大的模型,比如GPT2/3,加入差分隐私的机制将会一定程度上影响模型训练的效率
-
新的松弛:贝叶斯差分隐私
-
隐私学习和在线学习之间的关系
-
差分隐私和公平性:
联合隐私和公平的学习算法;
隐私和公平能够达到一致吗?
-
隐私,记忆和泛化:
扩展差分隐私
-
在语言模型中的隐私度量 [Zanella-Béguelin et al. 2020, Inan et al. 2021]
-
生成模型:
使用GAN去提取原始数据集[Cai et al. 2021]
-
联邦学习中的隐私